Loss Function

loss function은 classifier의 성능이 얼마나 별로인지를 나타내는 지표로 loss function의 값이 작을 수록 classifier가 train set을 정확하게 분류함을 의미한다. 일반적으로 loss function은 각 example에 대해 f(x,W)=x*W의 예측값과 실제 정답값인 yi를 loss function으로 비교하여 평균낸 값이다.
MultiClass Support Vector Machine (SVM) Loss

그 중에서도 multiclass svm의 loss function은 위와 같이 쓴다.

i번째 example xi에 대해 W에 따라 어떤 class로 분류될지에 대한 score을 구할 수 있고 이를 s라고 하자.
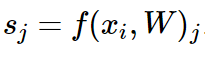
s_j는 xi가 j번째 class로 분류되는 것에 대한 score이다.
s_yi는 xi가 정답 label인 yi class로 분류되는 것에 대한 score으로 이것이 가장 높게 나와야 한다.
s_yi(correct class에 대한 score)은 s_j(incorrect class에 대한 score)보다 적어도 △만큼 커야 한다. (△는 hyperparameter)
따라서 s_yi > s_j + △, 즉 s_j - s_yi + △ < 0이라면 좋은 예측이고 이 때의 Loss는 0이다. 이를 yi를 제외한 모든 j에 대해 계산하여 합산한다.

위에서 s로 표시된 linear score function은 다음과 같으므로 이를 Loss function에 대입하면 loss function을 아래와 같이 다시 쓸 수 있다.
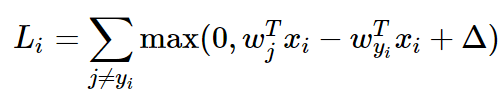
w_j는 W의 j번째 행에 해당한다.
hinge loss
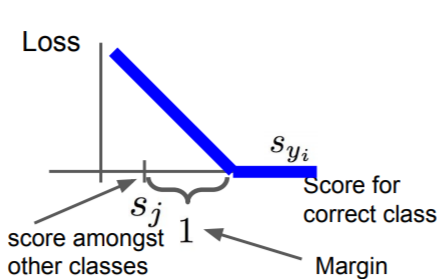
가로축을 s_yi라고 했을 때 s_yi가 sj에 비해 △(=1,margin)보다 크면 loss가 0이고, 그보다 작을 수록 loss 값이 증가한다. loss function이 hinge처럼 생겨서 multiclass svm loss를 hinge loss라고도 한다. 이렇게 0을 threshold로 두는 것을 hinge loss라고 한다.

squared hinge loss는 여기에 제곱을 한 값이다. squared hinge loss는 잘못 분류된 margin을 더 강하게 벌하는 방법이다. hinge loss는 안좋은 것에 패널티를 주는 것인데, squared hinge loss로 안좋은 것에 패널티를 훨씬 강하게 부여할 수 있다.
예시

L0 = max(0, 5.1-3.2+1) + max(0, -1.7-3.2+1) = 2.9 + 0 = 2.9
L1 = max(0, 1.3-4.9+1) + max(0, 2.0-4.9+1) = 0 + 0 = 0
L2 = max(0, 2.2 +3.1+1) + max(0, 2.5+3.1+1) = 6.3 + 6.6 = 12.9
L=(2.9 + 0 + 12.9)/3 = 5.27
Q1. car의 score가 조금 바뀌면 전체 Loss 값에 영향을 줄까?
A1. No. svm loss의 경우 정답 score 자체가 Loss에 영향을 준다기 보다, 정답 score가 오답 score와 얼마나 차이나는지가 Loss에 영향을 준다. 정답 score가 이미 오답 score와 차이가 많이 나므로 정답 score가 조금 바뀌어도 L1은 0으로 유지될 것이다.
Q2. Li의 min, max?
A2. Li의 최솟값은 0이고, 최댓값은 무한대이다.
Q3. W의 모든 s들을 작고 비슷한 값으로 initialize 하면, Li의 값은 어떻게 되는가?
A3. Li=∑max(0, s_j - s_yi + 1) ≒∑ max(0, 0+1) =∑1 = C-1이 될 것이다.
Debugging 방법으로 사용할 수 있다. W를 initialize 한 후 Li = C-1 이어야 bug가 없는 것을 확인할 수 있다.
Q4. Li=∑에서 yi도 포함하여 더하면 어떻게 되는가?
A4. Li=∑(j≠yi)로 sum 했을 때 L의 최솟값이 0이 나온다. j=yi일 때는 Li = 1이 되고, L의 최솟값을 1이 아닌 0으로 만들기 위해 yi를 포함하지 않고 더하는 것이다.

loss function은 training set에 대한 불행한 예측을 정량화 하는 함수이다.
correct class score과 incorrect class score은 △만큼 차이가 나야 한다. 이 때 loss가 0이 된다.
붉은 영역에 incorrect class score이 위치한 경우 loss가 쌓일 것이다.
이렇게 loss를 최소화 할 수 있는 W를 찾아야 한다.
Regularization

파란색 점을 training set, 흰색 점을 test set, 선은 Loss=0으로 만드는 W에 대한 model이라고 하자.
training set을 모두 정확하게 구분하여 L=0을 만드는 W는 유일하지 않다. W=0이면 λW 또한 0이 될 것이다.
training set에 fit하는 W는 매우 많을지 몰라도 test set에서도 Loss를 작게 만들어줄, data의 성능을 고려한 W를 찾아야 하고 이를 Regularization term에서 실현할 것이다. 이는 model이 최대한 단순한 W를 찾도록 해준다.
- model이 복잡해지지 않도록 model에 soft penalty를 추가한다: model이 복잡해 질 수록 감수해야 할 penalty가 많아진다.
- 좋은 W를 고르게 해준다.
- test set에 잘 fit 하도록 curve로 optimization을 해주어 simple 한 모델을 만든다.

loss function은 data loss와 regularization loss로 나눌 수 있다. data loss는 모든 example i에 대한 loss를 평균 낸 것이고 N은 모든 training example의 수이다. regularization loss는 regularization function에 hyperparameter λ을 곱한 것이다.
L2 Regularization

L2 norm으로 W에 대해 penalty를 주는 regularization 방법이고, 유클리디안 norm 또는 squared norm이라고 한다.
이 외에도 L1 norm을 사용한 L1 regularization, L1 norm과 L2 norm을 모두 사용한 Elastic net, Drop out, Batch normalization, Stochastic deptrh, fractional pooling 등의 방법이 있다.
L2 regularization vs L1 regularization

w1과 w2 모두 x와 내적했을 때 1이라는 동일한 값을 출력한다.
w1의 L2 penalty = 1^2 + 0 + 0 + 0 = 1,
w2의 L2 penalty = 0.25^2 + 0.25^2 + 0.25^2 + 0.25^2 = 0.25
L2 penalty에 따르면 w2가 더 좋은 parameter이다. (Loss function에 더 작은 값을 더하게 되니까)
반면, w1의 L1 penalty = 1,
w2의 L1 penalty = 0.25 + 0.25 + 0.25 + 0.25 = 1
L1 penalty에 따르면 w1과 w2이 동일한 성능의 parameter라고 판단한다. (하지만 일반적으로 L1 penalty는 w1이 더 좋은 parameter라고 판단한다.)
| L2 penalty | L1 penalty |
| - sparse 하고 작은 값들의 W을 선호한다. - W의 모든 요소들이 골고루 영향을 주길 원한다. |
- 0이 많은 W를 좋아하고, 0이 아닌 다른 요소들을 복잡하다고 생각함 |

모든 example에 대한 Loss function을 풀어 쓰면 위와 같다.
(1) Loss function 구하기: unvectorized version
def L_i(x, y, W):
delta = 1.0 # see notes about delta later in this section
scores = W.dot(x) # scores becomes of size 10 x 1, the scores for each class
correct_class_score = scores[y]
D = W.shape[0] # number of classes, e.g. 10
loss_i = 0.0
for j in range(D): # iterate over all wrong classes
if j == y:
# skip for the true class to only loop over incorrect classes
continue
# accumulate loss for the i-th example
loss_i += max(0, scores[j] - correct_class_score + delta)
return loss_i
xi에 대해 모든 class의 score을 구하여 loss function을 구한다. 0~D의 j class에 대해 loss function을 구할 때 for 문으로 구한다.
(2) Loss function 구하기: vectorized version
def L_i_vectorized(x, y, W):
delta = 1.0
scores = W.dot(x)
# compute the margins for all classes in one vector operation
margins = np.maximum(0, scores - scores[y] + delta)
# on y-th position scores[y] - scores[y] canceled and gave delta. We want
# to ignore the y-th position and only consider margin on max wrong class
margins[y] = 0
loss_i = np.sum(margins)
return loss_ifor문이 아닌 vectorization 방식으로 loss function을 구한다. j=yi일 때 sum하는 것을 막기 위해 margins[y]=0으로 yi를 모두 0으로 만들어준다.
Softmax (multinominal logistic regression)

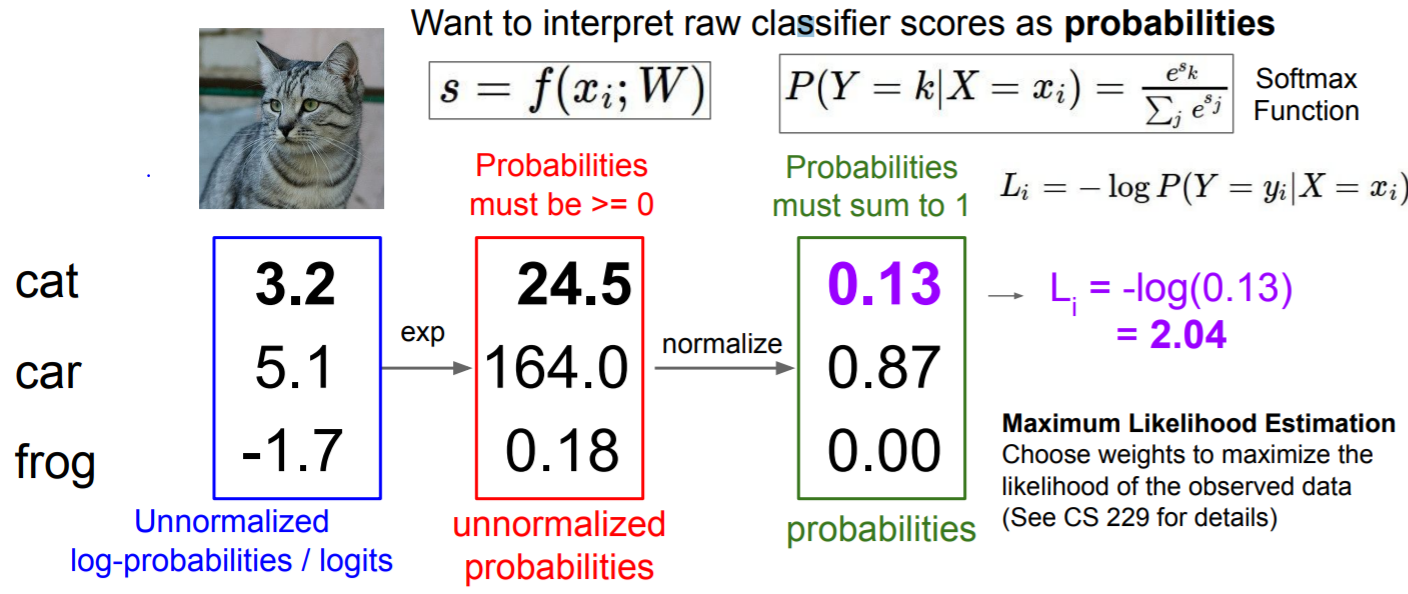
[3.2, 5.1, -1.7]의 score을 exp로 만들어서 [24.5, 164, 0.18]로 모두 양수가 되도록 한다. 이를 합했을 때 1이 되도록 normalize 시켜 전체 합으로 나눠서 [0.13, 0.87, 0.00]이 되도록 한다. 이 때 각 값이 0과 1 사이에 있고 합하면 1이 된다는 점에서 각각을 probability로 해석할 수 있고 이렇게 softmax function을 적용할 수 있다.
cross entropy loss
softmax classifier은 loss function으로 cross entropy loss를 사용한다. softmax 함수를 처리한 것에 maximum likeihood estimation에 따라 -log를 씌워 loss를 계산할 수 있다.
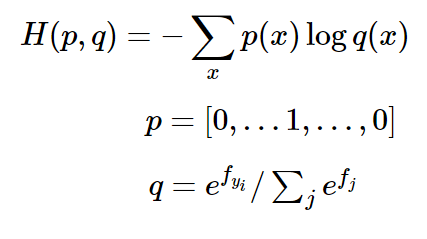
softmax classifier은 class에 대한 예측값 q (estimated distribution)와 실제 정답값인 p (true distribution)사이에서 cross entropy를 최소화 한다.
softmax 함수의 특징
- score을 probability로써 해석한다.
- class 별 확률분포를 알 수 있다.
- P(Y|X)=0이면 Li = -log 0 = ∞ (실제 무한대는 나올 수 없어서 overflow를 막기 위해 작은 상수를 더해준다.), 예측을 실패했을 때 loss가 커진다.
- P(Y|X)=1이면 Li = -log1 = 0으로 예측을 잘 했을 때 loss가 0이 나온다.
overflow

softmax를 계산할 때 exp가 값을 너무 크게 만들어서 값이 불안정 해질 수 있고 이를 overflow 문제라고 한다. 이를 방지하기 위해 softmax function의 분자, 분모에 상수 C를 곱하면 logC로 exp의 지수로 들어올 수 있다. 이렇게 logC를 지수에 더해도 softmax의 결과에는 영향을 주지 않을 것이다. 일반적으로 logC에 f_j의 최댓값을 넣어준다.
f = np.array([123, 456, 789]) # example with 3 classes and each having large scores
p = np.exp(f) / np.sum(np.exp(f)) # Bad: Numeric problem, potential blowup
# instead: first shift the values of f so that the highest number is 0:
f -= np.max(f) # f becomes [-666, -333, 0]
p = np.exp(f) / np.sum(np.exp(f)) # safe to do, gives the correct answer
f에 softmax를 그냥 처리하는 것보다 f의 최댓값을 빼주어 softmax를 출력하는 것이 좋다.
Q1. Li의 min, max
A1. Li=-log(P(Y|X))에서 P(Y|X)=0으로 잘못 예측하면 Li=∞이 된다. P(Y|X)=1으로 올바르게 예측하면 Li=0이 된다.
Q2. initialization 과정에서 sj가 모두 동일하게 작은 값으로 설정되면 Li는 어떻게 되는가?
A1. Li = - log (1/C) = loc C가 되고 debugging 과정에서 확인 가능하다.
Softmax vs SVM

softmax와 svm 방법 모두 데이터에 대해 f(x;w)=x*w로 score을 매겼지만 둘의 해석에 차이가 있다.
svm은 해당 class의 score이 오답 class의 score에 비해 얼마나 큰지 판단하고, 일정 수준 이상 크자면 성능 향상을 신경쓰지 않으므로 정답 class의 score이 바뀐다고 L이 크게 변하지 않는다.
softmax는 정답 class의 score이 달라지면 L도 변할 것이고 성능을 계속해서 향상시키려고 할 것이다.
위 예시는 같은 데이터에 대해 svm으로 계산했을 때는 loss가 1.58, softmax로 계산했을 때는 1.04가 나왔다.
Optimization
- loss를 최소화 하기 위한 적절한 W를 찾는 과정, gradient
(1) random search
임의의 W를 여러개 만들고 그 중 성능이 가장 좋은 W를 찾는 방법
시간이 아주 아주 오래 걸리고 구린 방법이다.
bestloss = float("inf") # Python assigns the highest possible float value
for num in range(1000):
W = np.random.randn(10, 3073) * 0.0001 # generate random parameters
loss = L(X_train, Y_train, W) # get the loss over the entire training set
if loss < bestloss: # keep track of the best solution
bestloss = loss
bestW = W
print 'in attempt %d the loss was %f, best %f' % (num, loss, bestloss)scores = Wbest.dot(Xte_cols) # 10 x 10000, the class scores for all test examples
Yte_predict = np.argmax(scores, axis = 0)
np.mean(Yte_predict == Yte)임의로 만든 1000개의 W 중 가장 성능이 좋은 W의 정확도는 15.5%였다. 다 찍어도 10%인데,,할말하않
(2) random local search
W = np.random.randn(10, 3073) * 0.001 # generate random starting W
bestloss = float("inf")
for i in range(1000):
step_size = 0.0001
Wtry = W + np.random.randn(10, 3073) * step_size
loss = L(Xtr_cols, Ytr, Wtry)
if loss < bestloss:
W = Wtry
bestloss = loss
print 'iter %d loss is %f' % (i, bestloss)임의의 W에서 시작하여 random 하게 δW을 설정, W의 loss보다 W+δW의 loss가 작으면 후자를 W로 재선택.
이 방법은 21.4%의 정확도가 나왔음. 여전히 낮다.
(3) following the gradient

-1) numerical gradient
def eval_numerical_gradient(f, x):
fx = f(x) # evaluate function value at original point
grad = np.zeros(x.shape)
h = 0.00001
# iterate over all indexes in x
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
# evaluate function at x+h
ix = it.multi_index
old_value = x[ix]
x[ix] = old_value + h # increment by h
fxh = f(x) # evalute f(x + h)
x[ix] = old_value # restore to previous value (very important!)
# compute the partial derivative
grad[ix] = (fxh - fx) / h # the slope
it.iternext() # step to next dimension
return gradf에 대한 x의 gradient를 구하는 함수다. 아주 작은 h(=0.00001)에 대해, x array의 모든 원소에 대해 (f(x+h)-f(x))/h를 구해서 grad에 넣을 것이다. 즉 x=(x1, x2, x3) 이면 grad의 x1 자리에 해당하는 원소는 (f(x1+h, x2, x3)-f(x1, x2, x3)) / h의 partial derivative가 된다.
centerd difference formula

f(x)의 양방향에서 미분값을 구하는 것이 더 나을 수도 있다.
CIFAR-10에서 loss function의 gradient 구하기
def CIFAR10_loss_fun(W):
return L(X_train, Y_train, W)
W = np.random.rand(10, 3073) * 0.001 # random weight vector
df = eval_numerical_gradient(CIFAR10_loss_fun, W) # get the gradientCIFAR-10에서 W의 초깃값을 설정하고, numerical gradient를 계산했다.
loss_original = CIFAR10_loss_fun(W) # the original loss
print 'original loss: %f' % (loss_original, )
# lets see the effect of multiple step sizes
for step_size_log in [-10, -9, -8, -7, -6, -5,-4,-3,-2,-1]:
step_size = 10 ** step_size_log
W_new = W - step_size * df # new position in the weight space
loss_new = CIFAR10_loss_fun(W_new)
print 'for step size %f new loss: %f' % (step_size, loss_new)original loss: 2.200718
for step size 1.000000e-10 new loss: 2.200652
for step size 1.000000e-09 new loss: 2.200057
for step size 1.000000e-08 new loss: 2.194116
for step size 1.000000e-07 new loss: 2.135493
for step size 1.000000e-06 new loss: 1.647802
for step size 1.000000e-05 new loss: 2.844355
for step size 1.000000e-04 new loss: 25.558142
for step size 1.000000e-03 new loss: 254.086573
for step size 1.000000e-02 new loss: 2539.370888
for step size 1.000000e-01 new loss: 25392.214036
CIFAR-10에서 random하게 설정한 W에 대한 loss function을 loss_original로 구했다.
step size를 10^(-10) ~ 10^(-1)로 설정하고 W에서 dL/dW * stepsize만큼 뺀 값으로 W를 다시 정하고 새로운 W 값으로 loss function을 다시 정해서 출력했다. step size가 커짐에 따라서 loss가 줄었다가 커졌다.
step size도 hyperparameter로써 설정해 줘야 한다,,,

위와 같이 CIFAR-10 data에서 W에 대해 아주 작은 h=0.0001으로 gradient dW를 계산할 수 있지만, 시간이 오래 걸린다는 단점이 있다.
-2) analytic gradient
미분을 이용하여 gradient 를 구할 수 있다.
Gradient Descent
while True:
weights_grad = evaluate_gradient(loss_fun, data, weights)
weights += - step_size * weights_gradW가 특정 값으로 수렴 할때까지 W를 step size * dW만큼 빼면서 계속해서 update를 시켜줄 수 있다.
| numerical gradient | analytic gradient |
| approximate, slow, easy to write | exact, fast, error-prone |
| => analytic gradient로 grad를 계한하고 numerical gradient로 에러가 있는지 체크하자. | |
mini-batch gradient descent
while True:
data_batch = sample_training_data(data, 256) # sample 256 examples
weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
weights += - step_size * weights_grad # perform parameter updatetraining set이 거대한 경우에 이를 모두 학습시키면 비용이 많이 들 수 있다. 그래서 training data 중 mini-batch만 뽑아서 학습을 시키면서 빠른 속도로 적절한 W를 찾을 수도 있다. 보통 mini batch size는 2^n개로 설정해야 빠르게 동작한다. mini batch의 gradient는 전체 관측치의 gradient에 대한 좋은 근사치이다.
Stochastic Gradient Descent (SGD)
한 번 W를 update 할 때 앞에서는 모든 example을 고려했는데, SGD에서는 한 개의 example로 W를 update 한다.
'딥러닝 > cs231n' 카테고리의 다른 글
| 3장. Programming: Stochastic Gradient Descent (0) | 2021.03.05 |
|---|---|
| 4장. Neural Networks and Back Propagation (0) | 2021.03.05 |
| 3장. Multiclass Support Vector Machine : Programming (2) | 2021.02.27 |
| 2강. Image Classification: Programming (0) | 2021.02.17 |
| 2강. Image Classification (0) | 2021.02.16 |



