학습 알고리즘의 역사
1. Perceptron

2. Multi Layer Perceptiron
- activation function을 이용하면서 여러 층을 쌓음
- sigmoid로 각 층으로 확률적 mapping 가능
- back propagation
3. Deep Multi Layer Perceptron
- sigmoid의 grad vanishing 문제를 ReLU로 해결
4. Deep Neural Network
- 음성인식, 영상처리에서 좋은 효과
- 뇌과학 연구에서는, 뇌가 시각정보를 받아들이는 데에 뉴런이 oriented edge와 shape에 반응하고 계층적 구조를 가진다는 것을 발견했다.
- LeNet-5: 우편물 숫자 인식
- AlexNet: imagenet classification
4. Convolutional Neural Network
- image classification, Retrieveal, Detection, Segmentation, self driving cars, pose recognition, image captioning ...에 응용
Fully Connected Layer

- Multi Layer Perceptron에서는 FC layer을 사용했음.
- input을 길게 펼치면 학습시 input의 공간성이 상실됨.
- 물체가 조금만 달라져도 새롭게 학습이 필요하고(translation invariant), overfitting이 잘된다.
- 학습해야 하는 parameter의 수가 매우 많다.
Convolution Layer
1) Filter
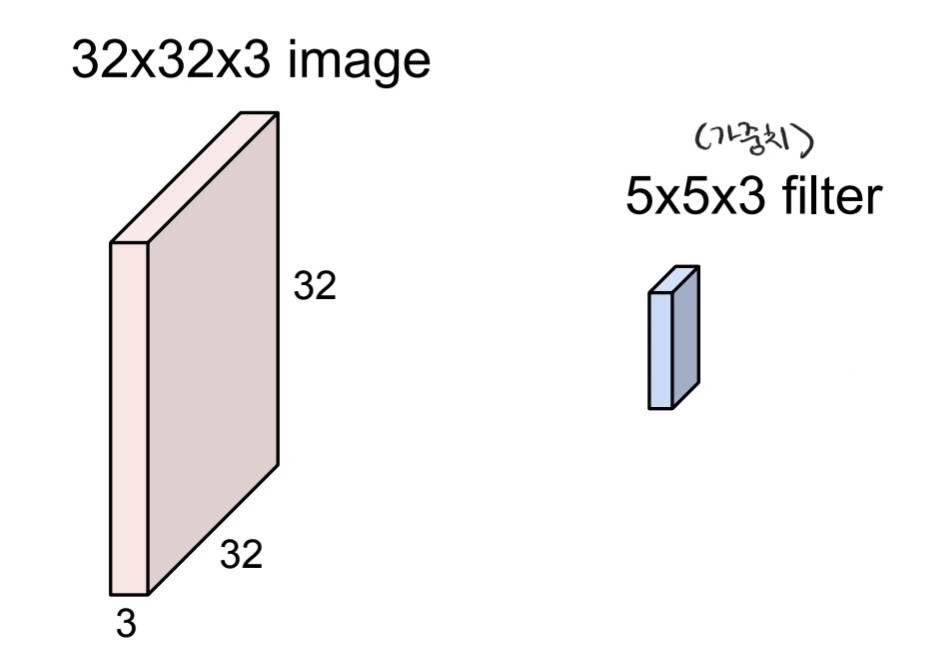
- input의 공간적 정보를 유지한다.
- filter: input을 슬라이딩하면서 input의 모든 요소들과 내적한다. w^t * x + b
- 격자구조를 갖는 데이터에 적합
- parameter 수가 줄어들어 overfitting의 가능성이 낮다.
- 한 층에 5*5*3+1개의 parameter
- 한 층에서 모든 노드가 paramter을 공유한다.
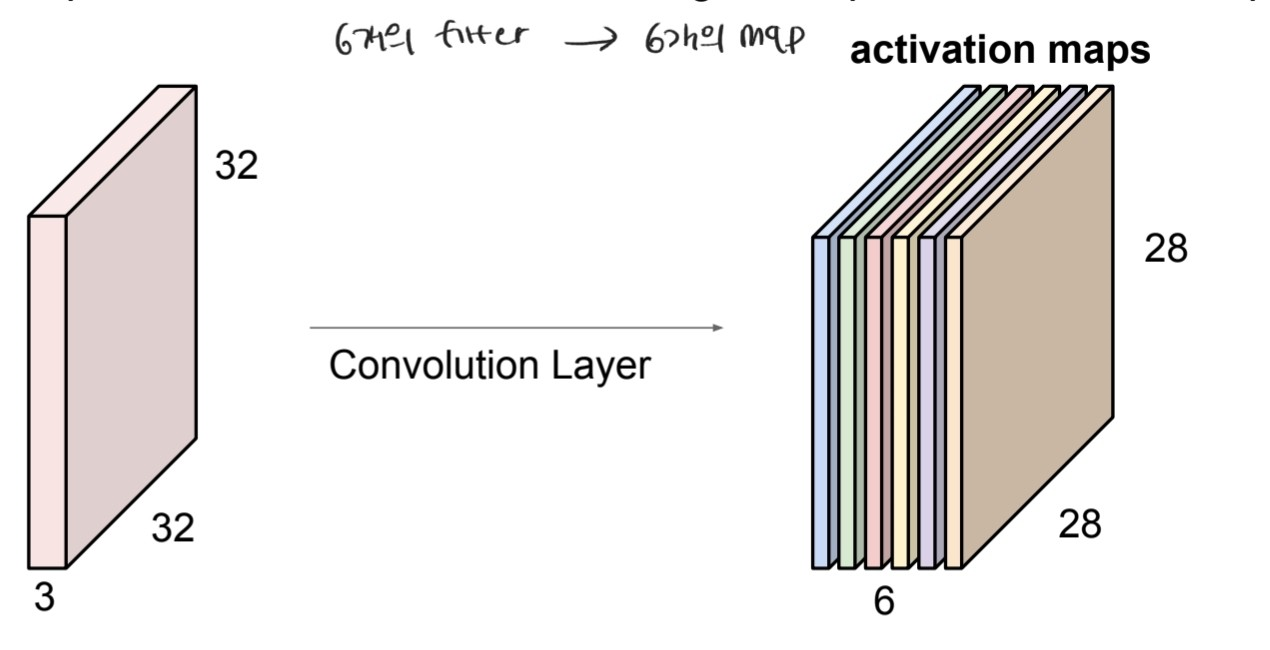
- filter의 수: 6개의 filter를 사용하면 6개의 activation map을 얻게 된다. (depth = 6)
CNN은 깊어질 수록 powerful 하다.

- CNN layer이 깊어질 수록 이미지의 단순한 특징에서(edge, corner, ...) 복잡한 특징(full object)을 뽑게 된다.
- 위 그림은 각 층의 activation map을 시각화 한 것인데, 이미지가 어떻게 생겨야 각 뉴런의 활성을 최대화 하는 지 나타낸 것이다.
2) Stride

- filter의 적용 위치 간격
- stride의 수가 커지면 output의 크기는 작아진다.
- input과 filter 크기에 따라 stride 크기가 조절되어야 한다.
3) Padding

- output 크기가 줄어드는 것 방지(input의 크기를 계속해서 유지함)
- input의 가장자리에 parameter가 적게 적용되는 문제 해결
output size와 parameter의 개수

총 paramter 수는 (F^2 * C + 1) * K개 이다.
CONV layer을 brain의 neuron 관점에서 생각하기
- CONV layer: 하나의 layer에서 filter은 input의 모든 지역을 처리한다.
- neuron: input의 local 한 지역만 처리한다.

- neuron은 한 번에 5*5개만큼의 input을 바라볼 수 있다.
- c.f) FC layer에서는 neuron이 전체의 input을 한번에 본다.
- 5개의 filter를 가지고 있을 때, 하나의 input에 대해 서로 다른 5개의 특징을 추출할 수 있다.
- 같은 input 지역을 바라보는 5개의 서로 다른 뉴런이 존재한다.
Pooling Layer
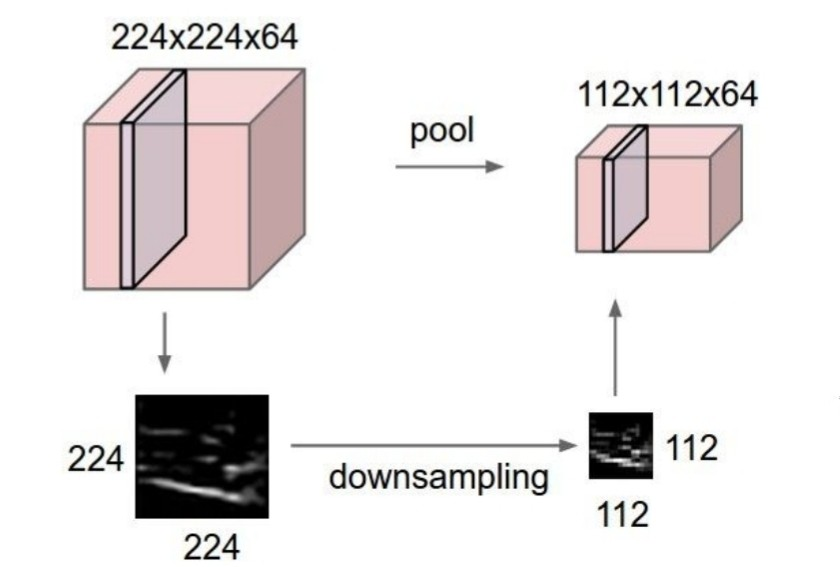
- downsampling: output의 size를 줄인다.
- parameter의 수를 줄이지만 depth는 줄이지 않는다.
- max pooling: 뉴런이 각 위치에서 얼마나 활성화 되었는지를 잘 나타냄
- average pooling 등 방법이 많지만 주로 max pooling 사용
- pooling 시에도 stride 사용 가능
- parameter가 필요하지 않다.
output size 계산

pooling layer에서 parameter는 필요하지 않다.

CNN architecture

[conv -> activation (ReLU) -> (pooling)] *M -> [fc -> relu]*K -> softmax
열로 보이는 그림은 각 layer에서의 activation map이다.
하위 계층에서 상위 계층으로 갈 수록 더 복잡한 feature를 얻게 된다. 하위 계층에서는 edge같은 단순한 구조가 얼마나 존재하는 지 찾고, 상위 계층에서는 더 복잡한 corner같은 구조를 찾는다.
각 layer의 input이 해당 그림과 비슷하게 생겼다면 점수가 높아진다. 마지막 pooling layer의 출력은 3차원 구조인데, 이를 1차원으로 펴준 뒤 fc layer에서 각 class에 대한 score이 출력된다.
'딥러닝 > cs231n' 카테고리의 다른 글
| FullyConnected Nets: Programming 개요 (2) | 2021.03.13 |
|---|---|
| 3장. Programming: Stochastic Gradient Descent (0) | 2021.03.05 |
| 4장. Neural Networks and Back Propagation (0) | 2021.03.05 |
| 3장. Multiclass Support Vector Machine : Programming (2) | 2021.02.27 |
| 3장. Loss Functions and Optimization (0) | 2021.02.18 |



