스캐터 플랏
* 데이터 준비
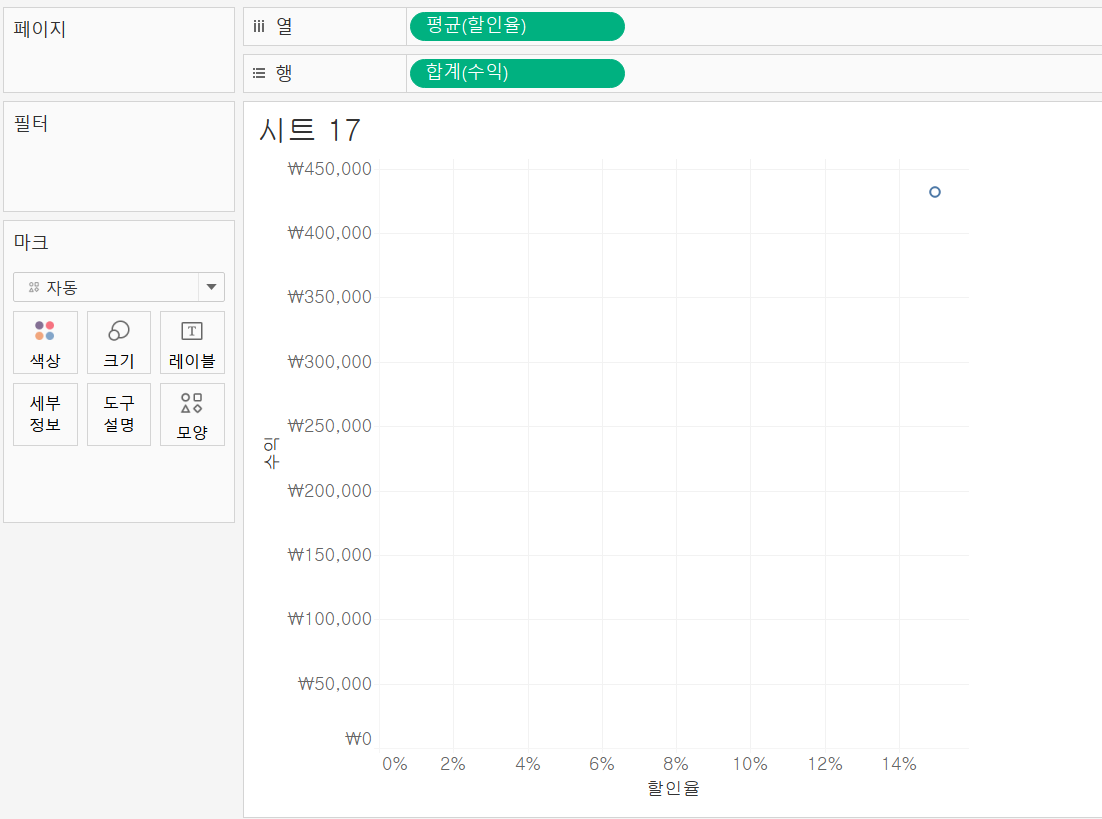
수익과 할인율의 관계를 알아보기 위해 수익과 할인율을 각각 더블클릭했다.
자동으로 수익은 합계로, 할인율은 평균으로 올라갔다. 측정값 필드 우클릭>기본속성>집계에서 or 열선반/행선반에서 알약 우클릭>측정값에서 확인할 수 있다.
시트의 그래프의 점은 모든 물품에 대한 할인율 평균과 수익 합계를 나타낸다.
고객별로 수익과 할인율의 관계를 파악하고자 '고객 이름'을 마크 안으로 넣어서 스캐터 플랏을 만들었다.
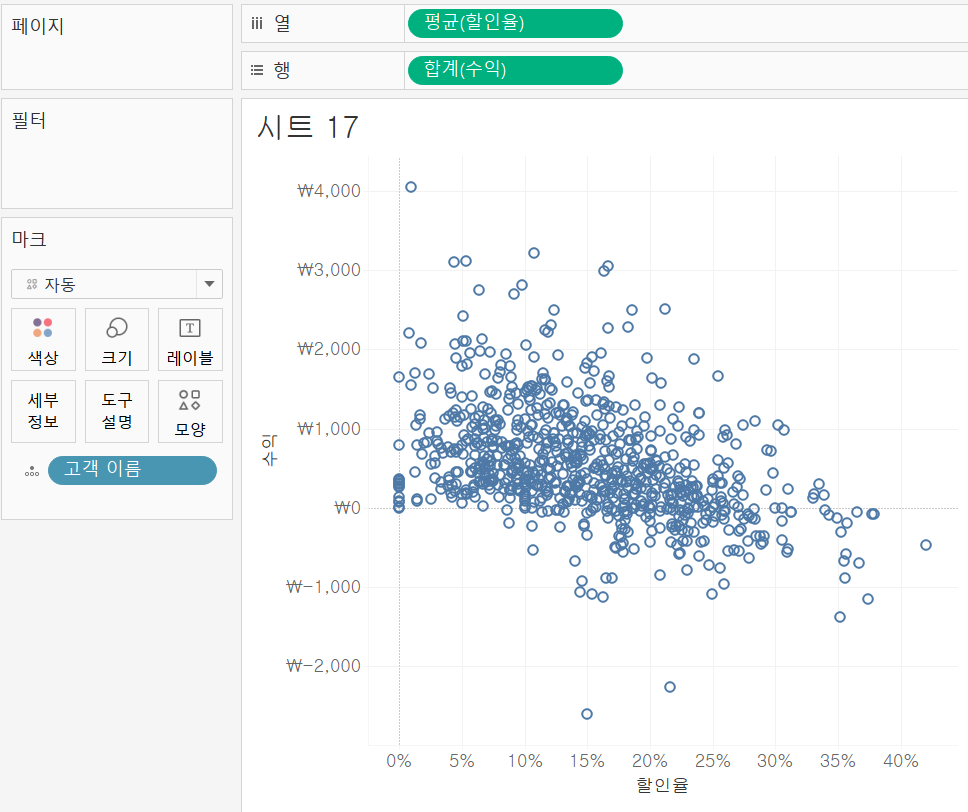
마크의 자동을 원으로 바꾸었다. 점은 한명 한명의 고객이 회사의 할인율과 수익에 어떤 관련이 있는 지에 대한 것이다.
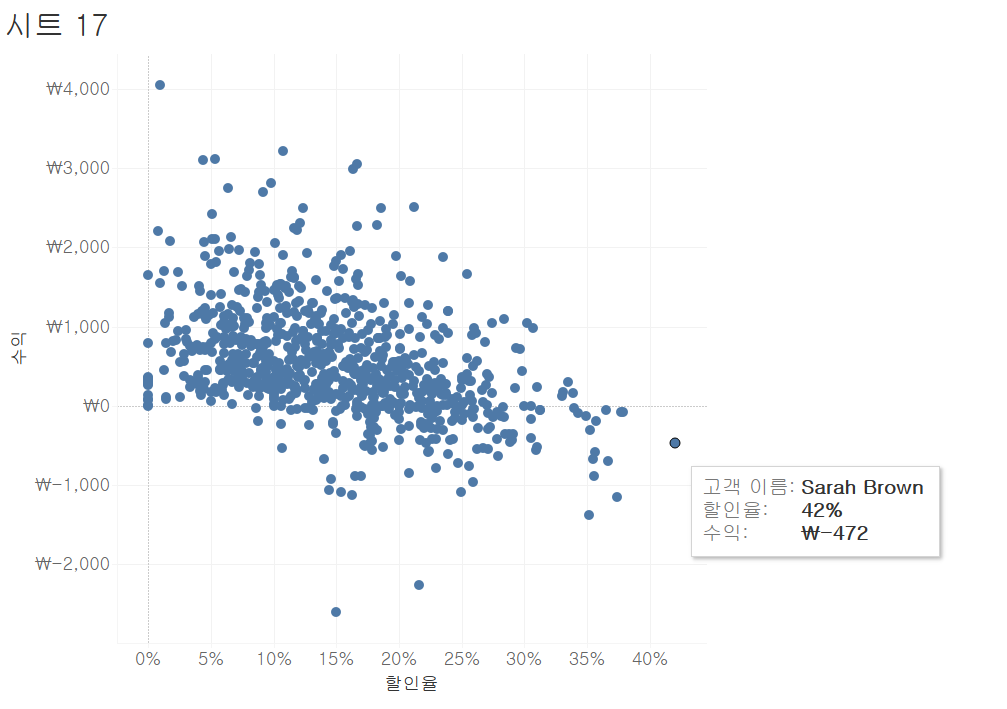
<눈에 잘 들어오는 스캐터 플랏 만들기>
(1) 점의 색상/불투명도/테두리 변경
마크>색상>에서 색상/불투명도/테두리를 변경한다.
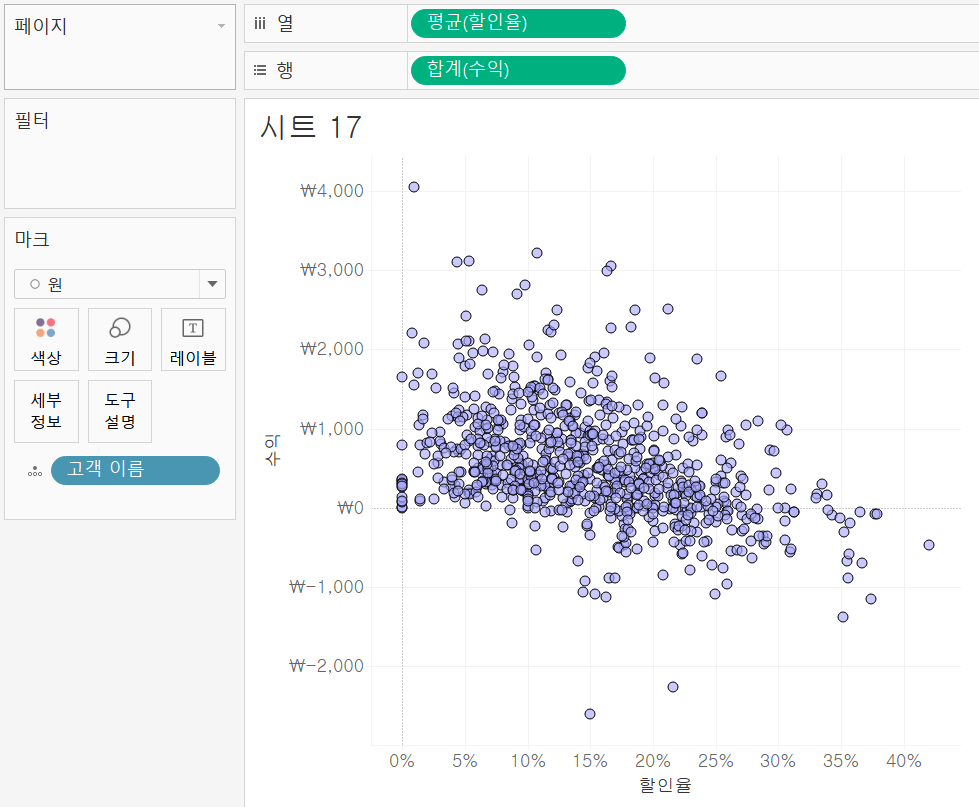
(2) 변수 추가하기
어떤 고객이 수익에 어떤 영향을 끼치는지 파악하려고 한다. 수익을 마크>색상에 올렸다.
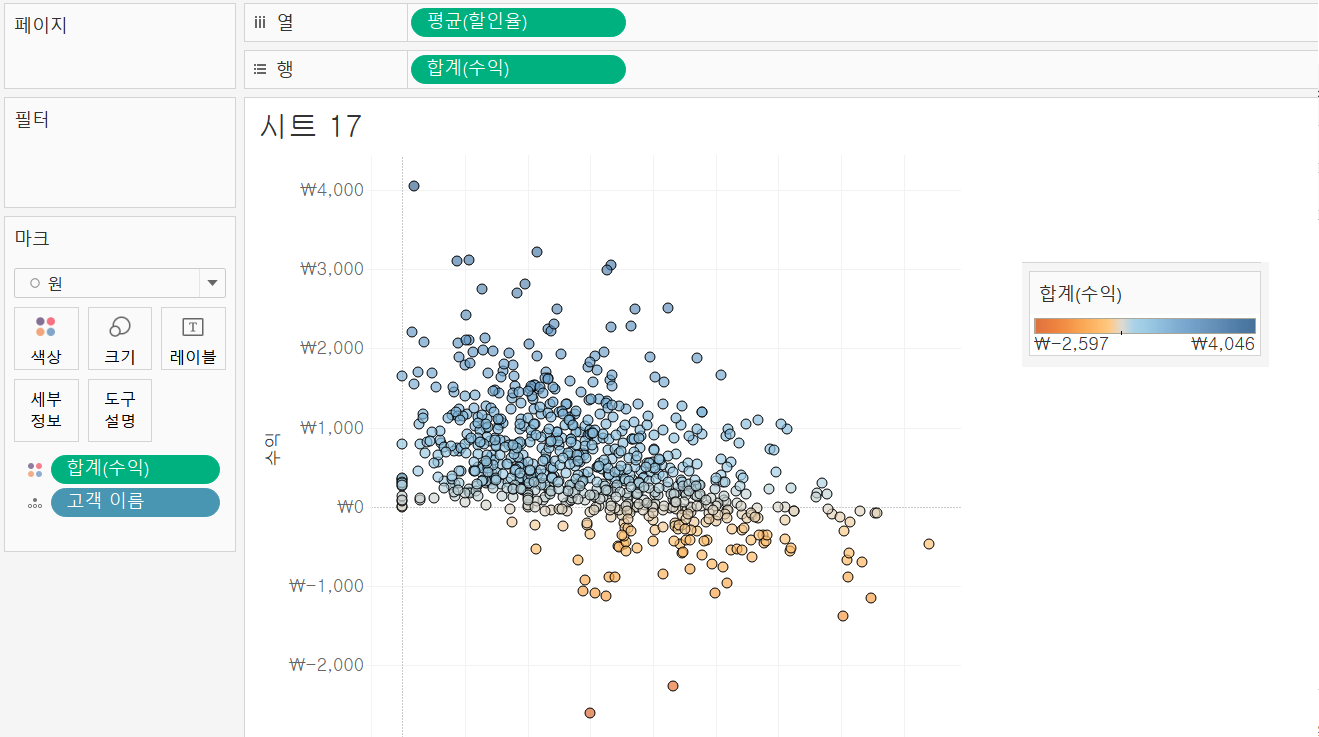
(3) 방금 올린 변수를 다른 변수로 대체
고객별 수익과 할인율의 관계가 아닌 제품별 수익과 할인율의 관계를 파악하기 위해 마크 필드에서 고객 이름 대신 제품 이름을 넣어준다.

(4) outlier 없애기
제거하고 싶은 outlier 점을 우클릭>제외
(5) 추세선 그리기

왼쪽의 분석 탭에서 추세선을 시트 안쪽으로 끌고 들어오면 그릴 추세선의 종류가 나온다. '선형'을 클릭하여 선형 추세선을 그렸다.
히스토그램
동영상에선 profit bin과 record 수를 변수로 올렸는데, 변수를 못찾겠기도 하고, 대체할 만한 변수를 못찾아서 동영상 캡쳐로 대체하겠다.
* 구간차원 설정
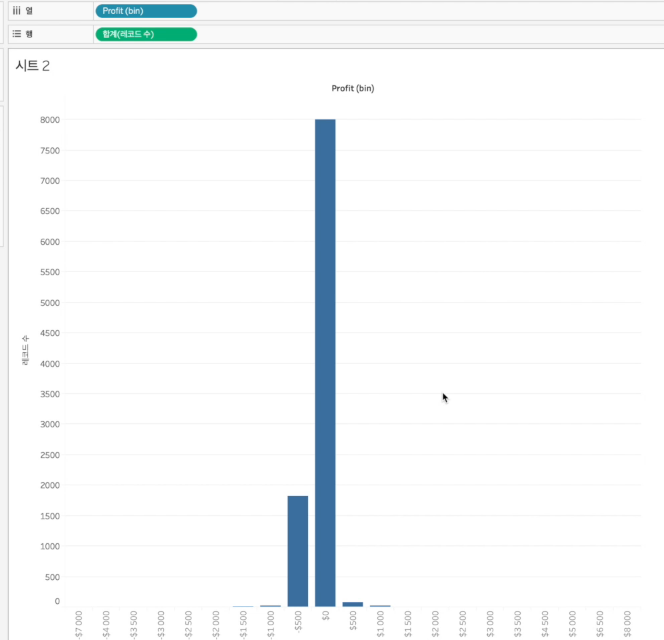
profit(bin)을 열선반에, 레코드 수를 행선반에 올린 결과이다. 0달러 근처에 데이터가 몰려있는데 바 하나의 너비가 너무 좁고 bar가 너무 촘촘하다.

테이블에서 측정값 필드 우클릭>만들기>구간차원>구간차원 크기를 200에서 500으로 바꿔줘서 bar의 너비를 조정했다.
=> 원하는 필드에 대해 직접 구간차원을 설정할 수 있다.
* sales 변수 구간차원 설정하기
측정값 필드 우클릭>만들기>구간차원>구간차원 크기 1000으로 바꾸기
sales(구간차원)이라는 변수를 새로 설정하고 열선반에 올리고, 레코드 수를 행선반에 올려서 sales(구간차원) 별 레코드 수를 본다.

박스 플랏
제품의 중분류 별 수익을 파악하기 위해 수익을 행선반에 올리고 중분류를 마크>세부정보 위에 올렸다. bar가 중분류에 따라 잘게 잘라졌고 잘린 박스에 마우스를 가져다 대면 제품의 중분류에 따른 수익이 나온다.

마크를 막대가 아닌 원으로 바꾸면 제품의 중분류별로 수익이 줄세워져서 나타난다.
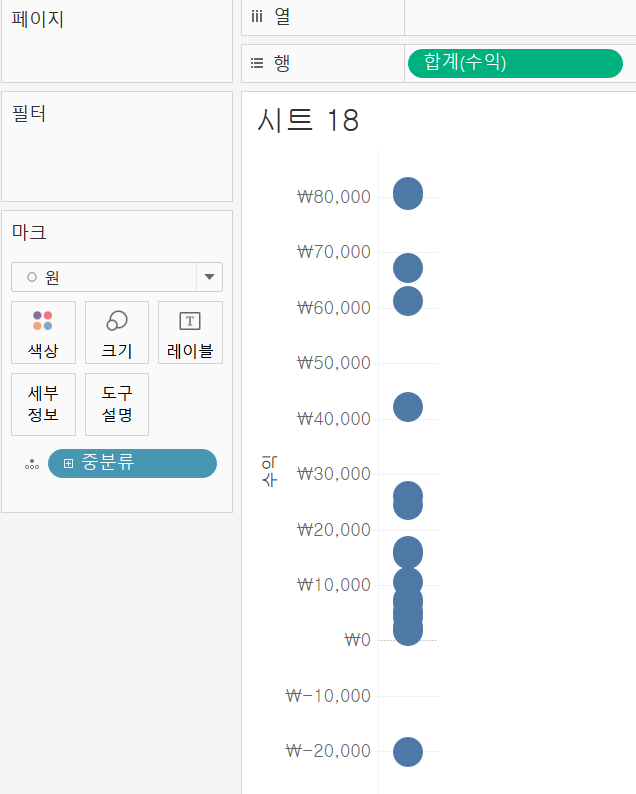
표현방식을 박스플랏으로 바꿔주었다.

아래에서부터 박스의 시작 라인인 Q1은 제품을 수익 낮은 순으로 줄세웠을 때의 1/4 지점, 박스 중간 라인인 Q2는 중앙값, 박스의 끝 라인인 Q3은 3/4지점을 의미한다. 가장 높은 지점은 Q4로 4/4 지점이다.
지역에 따른 제품의 중분류별 수익을 파악하기 위해 '지역'을 열선반에 올렸다.

북아시아는 제품별로 수익이 크게 차이나는 반면, 오세아니아는 제품별 수익별 편차가 적다.
IQR은 Q3-Q1로 박스 안의 모든 점에 해당한다.
어떤 점이 Q3+1.5*IQR 위에 찍혀 있거나 Q1-1.5*IQR 아래에 찍혀 있으면 그 점은 outlier에 해당한다.
* 모든 점을 박스플랏 안에 포함시키기
어떤 점이 outlier인지에 관심이 없고, 모든 점을 박스플랏 안에 포함시키고 싶으면 박스플랏 우클릭>편집>수염 확장>최대 데이터 범위로 바꿔주면 outlier이 있던 박스플랏의 수염의 길이가 늘어난다.

* outlier 중점적으로 확인하기
outlier만 중점적으로 확인하고 싶다면, 박스플랏 우클릭>편집>수염확장>IQR 1.5배 내 데이터 상태에서 기초마크 숨기기 옵션을 선택하면 박스 안의 점들은 생략되고 outlier만 박스 바깥에 점으로 표시된다.
어떤 관측치가 통상적인 관측 범위를 벗어나는 지 확인할 수 있다.

'시각화 > tableau 기초' 카테고리의 다른 글
| 태블로 기초: 차원과 측정값 (0) | 2021.04.04 |
|---|---|
| 태블로에서 차트 그리기 ④ 하이라이트 테이블(히트맵)과 기타 차트 (0) | 2021.04.04 |
| 태블로에서 차트 그리기 ② 비율을 나타내는 차트: 파이차트 & 비율 바차트 (0) | 2021.04.03 |
| 태블로에서 차트 그리기 ① 바 차트와 라인 차트 (3) | 2021.04.03 |
| 태블로 기초 리뷰 ③ 태블로 작업창 살펴보기 (2) | 2021.03.31 |



