https://theeffectbook.net/ch-StatisticalAdjustment.html?panelset=python-code&panelset1=python-code2&panelset2=python-code3
해당 내용은 위 링크를 참고하여 작성했습니다.
상호작용항
:Y와 X의 관계가 X가 아닌 Z에 의해 변화한다면?
$Y = \beta_0 + \beta_1X + \beta_2Z + \beta_3XZ + \epsilon$
- e.g. 휘발유 가격(X)과 주행 마일(Y)의 관계는 자동차 소유 여부(Z)에 의해 달라짐 → X와 Z의 상호작용 관계까지 변수에 추가해야 함
Interaction Terms의 해석 (1) - X가 Z와 상호작용 효과가 있을 때, X의 효과는 어떻게 해석해야 하는가?
- Y에 대한 X의 derivative: Y에 대한 X의 효과
- Y에 대한 X의 효과에는 X의 단일 효과는 포함되지 않음
- 주어진 Z 값에서 X의 효과를 파악해야 함
- e.g. Z = 0일 때 X의 효과: $\beta_1$, Z = 16일 때 X의 효과: $\beta_1+16\beta_3$
- → $\beta_1$을 “Y에 대한 X의 효과”라고 볼 수 없음
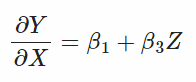
Interaction Terms의 해석 (2) - Interaction Term 자체의 해석
- Y에 대한 X와 Z의 derivate: interaction term 자체의 효과
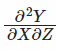
- $\beta_3$(Z의 계수)에 대한 해석: Y에 대한 X의 derivative에서 확인할 수 있듯이 ($dY/dX = \beta_1 + \beta_3Z$), “Z가 한단계 변화할 때 Y에 대한 X의 효과가 얼마나 강력한 지”로 해석할 수 있음
Z가 이진변수일 때
$Y = \beta_0 + \beta_1X + \beta_2Child + \beta_3XChild + \epsilon$
- $Child$: binary variable
- Y에 대한 X의 효과 = $\beta_1 + \beta_3Child$
- $Child = 0 → \beta_1$
- $Child = 1 → \beta_1 + \beta_3$
- $\beta_3$: $Child$ 여부에 따른 Y에 대한 X의 효과의 차이. 즉, “NonChild에 비해 Child일 때 Y에 대한 X의 효과가 얼마나 강력한 지”로 해석 가능 → NonChild와 Child 사이의 Y에 대한 X의 효과
상호작용항 해석 예시
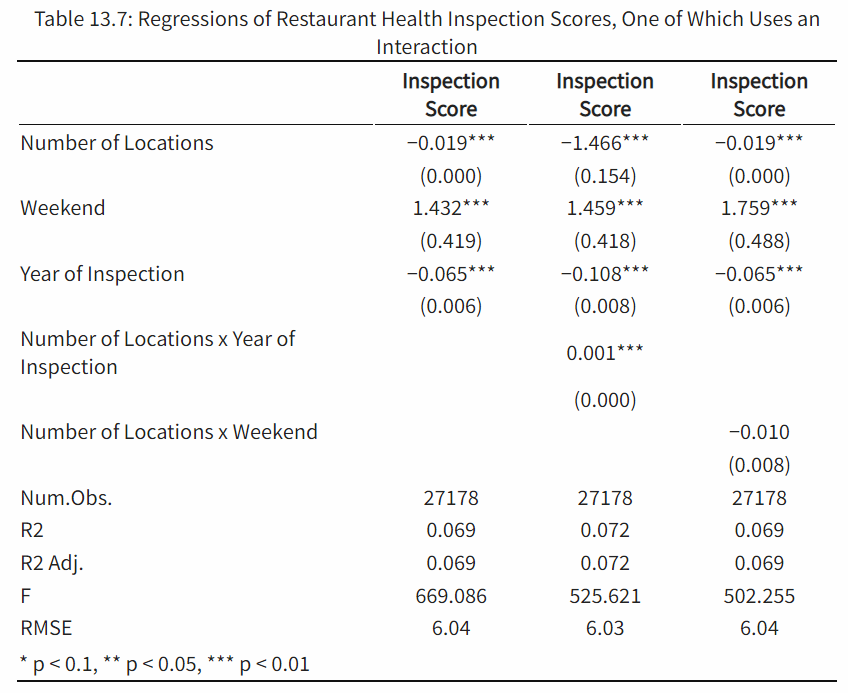
- model 1: Inspection Score = Number of Locations + Weekend + Year of Inspection
- model 2: Inspection Score = Number of Locations + Weekend + Year of Inspection + Number of Locations * Year of Inspection
- model 3: Inspection Score = Number of Locations + Weekend + Year of I nspection +Number of Locations * Weekend
모델 해석
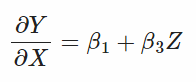
- model 2
- Number of Locations: Inspection of Year = 2008일 때 Number of Location이 1단위 늘어나면 Inspection Score이 -1.466 + 0.001 * 2008 = 0.542만큼 평균적으로 상승함.
- Number of Locations의 coefficient는 -1.466으로 음수이지만, 결과적으로는 Y에 대해 양의 상관관계를 가진다.
- model 3
- non-weekend일 때 Number of Location이 1단위 늘어나면 Inspection Score이 -0.019만큼 평균적으로 감소함
- weekend일 때 Number of Location이 1단위 늘어나면 Inspection Score이 -0.019 - 0.010 = -0.029만큼 평균적으로 감소함
상호작용항 사용 시 주의점
- (1) 상호작용항을 왜 사용하려는지 목적을 분명히 하라
- 상호작용항을 추가했을 때 유의미한 결과가 나오더라도, 그건 subgroup에게만 해당되는 내용일 수도 있음. 그리고 그 subgroup은 아주 specific 할 수 있기에, 데이터를 면밀히 확인하기 전에 상호작용항을 추가하는 것은 좋지 못한 선택임.
- (2) 상호작용항이 생기면 그렇지 않을 때에 비해 (통계적 검정력을 갖기 위한) 데이터가 훨씬 많이 필요함
- 상호작용항의 유의성이 단순히 sampling variation 때문일 수도 있음
'계량경제학 > 인과추론의 데이터과학' 카테고리의 다른 글
| 인과추론을 위한 회귀분석 - Standard Error을 어떻게 고치면 되는가? (1) | 2022.09.25 |
|---|---|
| 인과추론을 위한 회귀분석 - Standard Error의 정의와 가정 (1) | 2022.09.25 |
| 인과추론을 위한 회귀분석 - 변수 변환 (1) | 2022.09.21 |
| 인과추론을 위한 회귀분석 - Polynomials (1) | 2022.09.21 |
| 인과추론을 위한 회귀분석 - Discrete Variable (2) | 2022.09.21 |



