인과추론을 위한 회귀분석 - Polynomials

https://www.notion.so/Regression-263a1a5f472c49189a8e7ceb6d8f623d

 

해당 내용은 위 사이트를 참고하여 작성했습니다. 

---

Polynomials

• OLS는 종속변수가 독립변수 사이 관계가 선형으로 설명된다고 가정함. 아래와 같이 종속변수와 독립변수 사이가 선형으로 설명되지 않을 때에도, 추가 과정을 통해 OLS를 적합할 수 있음
  • (1) model에 Polynomial term을 추가하기
  • (2) data를 transform 하기

종속변수와 독립변수가 선형으로 설명되지 않는 예시

 

(1) coefficient의 해석 방법

$Y =\beta_1X + \beta_2X^2+\beta_3X^3$

• $\beta_1$: 나머지 변수들이 constant 할 때 $X$가 한단계 변화할 때 $Y$의 변화량의 평균 → $X$의 변화는 $X^2$, $X^3$의 변화를 동반하기 때문에 이러한 해석은 틀렸음

• $X$가 한단계 변화할 때 $Y$의 변화량을 $Y$의 $X$에 대한 derivate으로 해석하여, $X$가 한단계 변화할 때 $Y$는 $\beta1 + 2\beta_2X + 3\beta_3X^2$만큼 unit으로 변화한다고 해석

(2) 그렇다고 너무 많은 다항식 항을 추가하는 것이 좋은건 아님

데이터에 더 잘 적합시키기 위해 3차, 4차, 5차, …. 식을 계속해서 추가한다면

(1) model을 해석하기 점점 어려워짐

(2) 많은 경우에 차수가 늘어난다고 해서 데이터를 더 잘 적합하게 되는 것은 아님

2차식과 3차식이 큰 차이가 없음

 

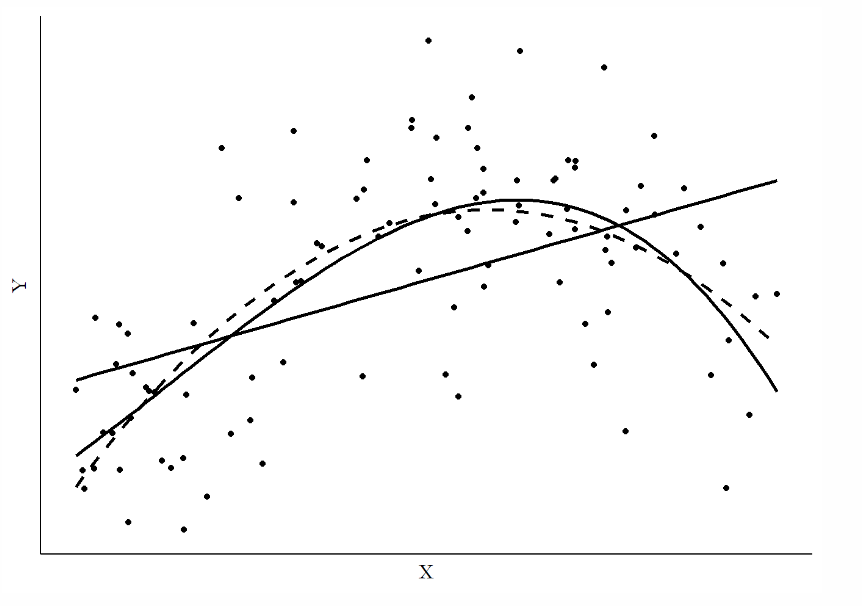
(3) overfitting의 문제 - 모델이 데이터의 작은 변화에 민감하게 반응하고, 관측된 데이터의 가장자리 근처에서 이상한 예측을 할 수 있음

10차식을 적합시켰을 때, 데이터의 우측에서 이상하게 예측함

 

적절한 차수를 찾는 방법?

(1) data를 시각화하고 낮은 차수부터 적합시켜보기

(2) residual을 시각화하기

(좌측) 1차항 적합시에는 X와 residual 사이에 곡률이 생성되지만, (우측) 2차항 적합시에는 X와 residual의 관계는 그저 noise로 보임 → 2차항에서 적합을 멈출 수 있음

 

• 다항식 항이 충분하다면, X와 residual 사이에 관계가 없어야 함 → residual plot에서 X와 residual 사이에 관계가 없어질 때 까지 차수를 늘릴 수 있음
• 주의사항: statistical significance를 근거로 차수를 선택하면 안됨