https://theeffectbook.net/ch-StatisticalAdjustment.html
해당 내용은 위 링크를 토대로 작성되었습니다.
error term의 iid 가정이 깨졌을 때 취할 수 있는 방법들을 알아보자.
Hetero-skedasticity가 있을 때의 문제점
- error term $\epsilon$의 분산이 X의 값에 따라서 달라지는 경우
- Standard error을 계산할때 분산이 더 높은 영역에서 Y의 조건부 평균이 왔다갔다함 → 일반 OLS 표준편차는 분산이 높은 영역의 표준편차를 따로 계산하는 것이 아니라, 전체 범위에서의 표준편차를 계산하기 때문에 표준편차를 과소평가 하게 됨
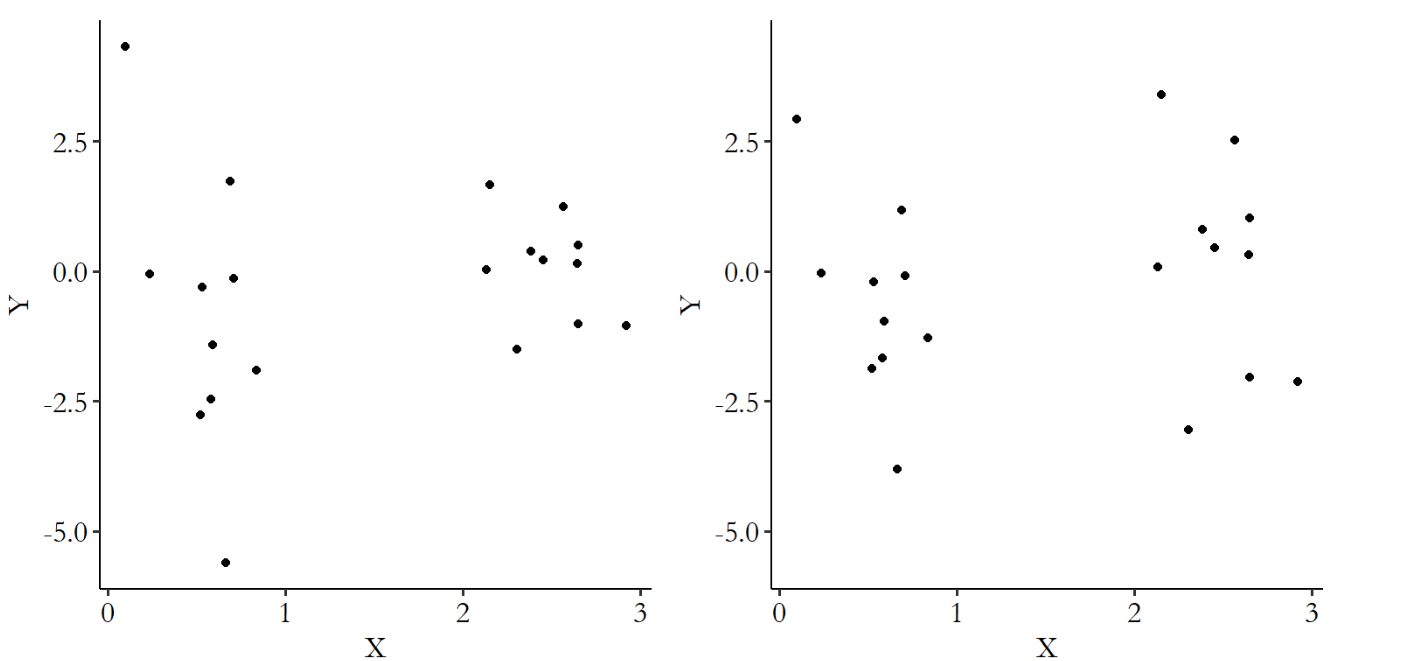
(왼쪽 플랏부터 A, B라고 할 때) A, B는 전체 X 범위에서 Y의 표준편차가 동일하지만
- A: 왼쪽 클러스터의 Y의 표준편차 > 오른쪽 클러스터의 Y의 표준편차(X가 커짐에 따라서 error term의 분산이 줄어듦), 즉 heteroskedasticity가 있음.
- B: 전체 X 범위에서 Y의 표준편차가 비슷함
=> 보통 Sandwich Estimator form을 통해 계산함
Sandwich Estimator
- model에 heteroskedasticity가 있는 경우, estimator은 아래와 같이 복잡한 형태로 추정되어야 함
- $(X'X)^{-1}(X'\SigmaX)(X'X)^{-1}$
- S의 type에 따라 Sandwich Estimator의 type이 달라짐
- c.f.) 일반적인 OLS의 estimator: $\hat{\beta}_{OLS} = (X^TX)^{-1}X^TY$
(1) Huber-White method
- heteroskedasticity를 해결하기 위한 sandwich estimator method으로, robust standard error을 계산하는 대표적인 방법임
- heteroskedasticity-consistent (HC) standard error이라고도 함
- 각 관측치의 잔차를 제곱후, 해당 제곱한 잔차를 가중치로 적용해 스케일링 → 분산을 계산할 때 잔차가 큰 관측치에 가중치를 부여함
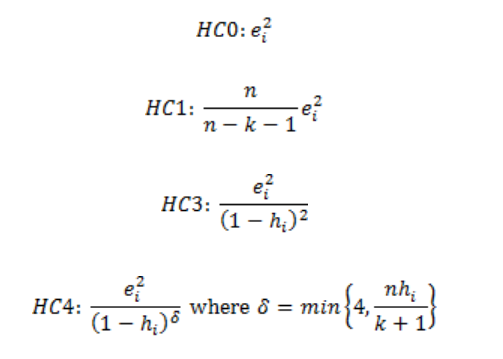
import statsmodels.api as sm
model = sm.OLS(y, x).fit(cov_type='HC0') # 'HC0', 'HC1', 'HC2', 'HC3'(2) Newey-West estimator
Correlated Error
- error term에 independency가 있어서 error 간 correlation이 있을 때
- 추정량의 sampling distribution을 변경시킬 수 있음
- e.g.) 사람들의 키를 측정할 때
- (i) 전세계 사람들을 무작위로 추출하여 키를 측정할 때 → sampling distribution에 대해 특정한 standard deviation을 얻을 수 있음
- (ii) 가족 단위로 사람들을 추출하여 키를 측정할 때 → 가족 간 키에 상관관계가 있음 → sampling distribution에 대한 standard deviation이 커짐
temporal autocorrelation이 있을 때
- Heteroskedasticity & Autocorrelation-Consistent (HAC) standard errors 사용
- Newey-West estimator
import statsmodels.api as sm
model = sm.OLS(y, x).fit(cov_type='HAC', cov_kwds={'maxlags': n})
spatial autocorrelation이 있을 때
- Conley spatial standard error을 사용함
(3) clustered standard error
hierarchical structure
- e.g.) 학생들에게 노트북을 제공하는 것 → 시험 점수에 미치는 영향을 회귀분석 하고 싶을 때, 오류가 교실 내에 클러스터 되어 있음
- → clustered standard error를 적용함
- Liang-Zeger Standard Error
- 교실별로 cluster를 다르게 지정해주어서 cluster 내의 X들간 상호작용하도록 함
- 적절한 범위로 클러스터를 지정하는 것이 필요함 (개인별 클러스터 - 너무 작음, 교실별 클러스터 - 적절함, 학교 별 클러스터 - 너무 큼)
- 적절한 범위를 찾기 위한 방법
- 컨셉에 따라 범위를 나눔 (e.g. 교실별로 결과가 다르게 나타나는 지가 중요한 문제일 때, 교실별로 클러스터링)
- treatment 수준에 따라 범위를 나눔 (e.g. 랩탑이 주어진 교실들 vs 랩탑이 주어지지 않은 교실들)
'계량경제학 > 인과추론의 데이터과학' 카테고리의 다른 글
| 인과추론을 위한 회귀분석 - Sample Weights (0) | 2022.10.03 |
|---|---|
| Gauss-Markov Assumptions (0) | 2022.09.30 |
| 인과추론을 위한 회귀분석 - Standard Error의 정의와 가정 (1) | 2022.09.25 |
| 인과추론을 위한 회귀분석 - 상호작용항 (0) | 2022.09.21 |
| 인과추론을 위한 회귀분석 - 변수 변환 (1) | 2022.09.21 |


