Binary classification

사진이 고양이인지(1) 아닌지(0)를 분류하기 위한 neural network를 만들려고 한다.
이진 분류 문제(binary classification)는 machine learning model 중 logistic regression을 사용하면 된다.
input data는 사진이기 때문에 사진의 색깔을 64*64 행렬의 r,g,b 값을 3차원의 array로 받는다.
이를 하나의 길다란 벡터로 만들어서 사용한다. nx는 벡터로 만든 input data의 길이로, 여기선 64*64*3=12288이 된다. 이 X 벡터를 neural network 안에 넣어서 y(0 또는 1)을 예측할 것이다.
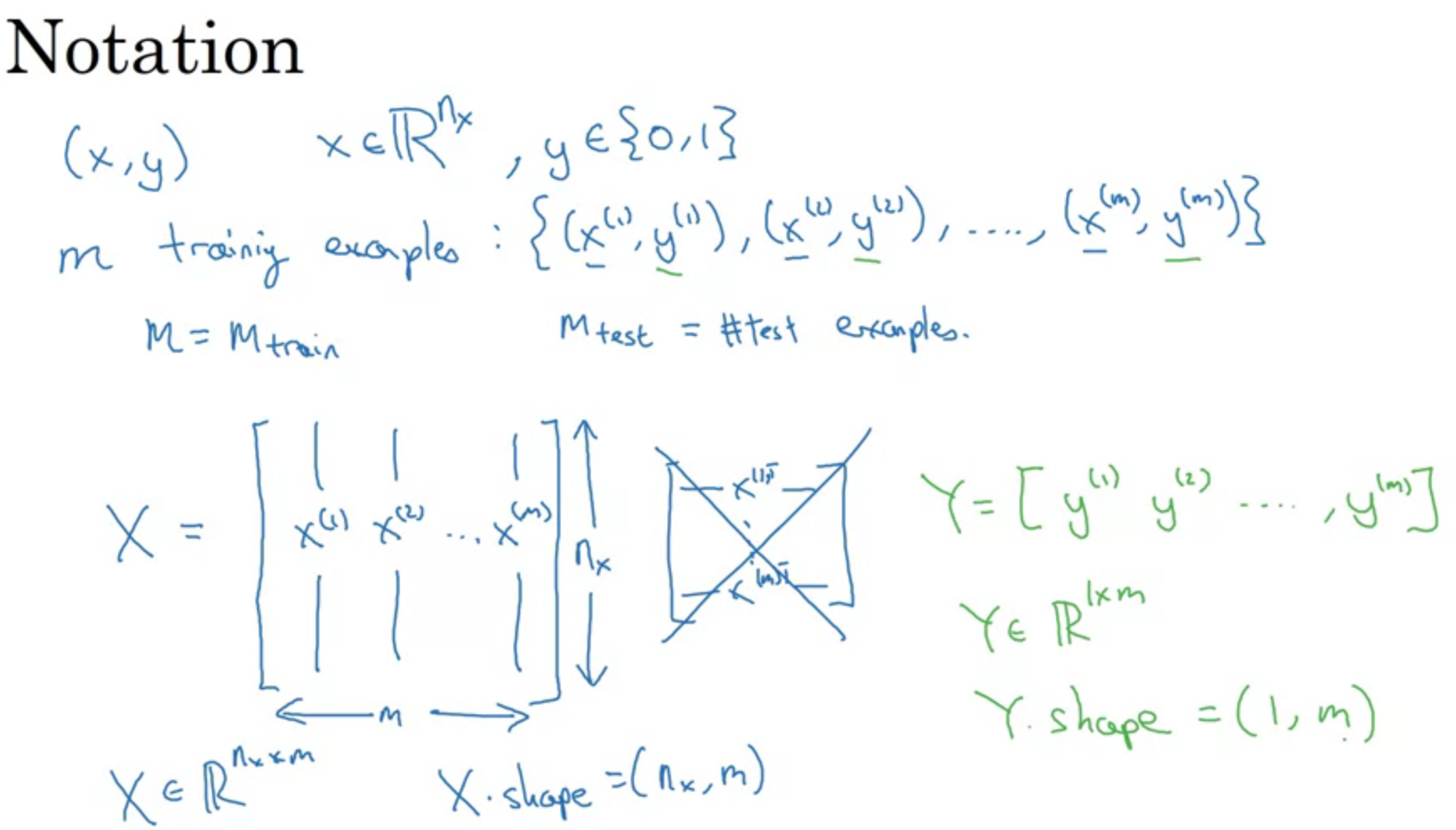
하나의 example에 대해서 X는 nx*1짜리 벡터이다.
우리는 여러개의 example을 한 번에 input으로 받을 것이다.
m개의 example에 대해 처리를 한다고 했을 때 X 안에 x(1)부터 x(m)까지 벡터들을 놓을 것이고 이 때 X.shape은 nx*m이 된다. (machine learning에서는 x(1)~x(m)벡터들을 가로로 쌓았는데 여기선 다르다)
Y도 x(1)~x(m)에 대한 예측을 내놓아야 하니 y(1)~y(m)을 원소로 가지는 벡터가 될 것이고 Y.shape은 1*m이 될 것이다.
Logistic Regression

(binary classification에서 )ŷ는 주어진 x에 대해 y=1일 확률을 의미한다. 즉 y가 0또는 1 둘 중 하나의 값만을 가지는 것과 달리 ŷ는 0에서 1 사이의 확률을 의미한다. ŷ이 1에 가까울 수록 y=1일 확률이 높은 것이고, ŷ이 0에 가까울 수록 y=1일 확률이 낮은, y=0일 확률이 높은 것이다.
하나의 example에 대해서만 생각한다면 x는 nx*1짜리 벡터이고 y는 0또는 1의 실수, ŷ는 0에서 1 사이의 실수이다.
ŷ는 x에 parameter w를 곱하고 b를 더해준 값에 activation function, 여기서는 sigmoid function을 처리해 준 값이다.
sigmoid function은 자연상수를 이용하여 정의한 함수인데, σ(z)에서 z가 클 수록 1에 가까운 값을 가지고 z가 작을 수록 0에 가까운 값을 가지는 함수이다.
Logistic Regression Cost Function

x(i)에 대해 ŷ(i)는 x(i)*w(t)에 b를 더해준 후 sigmoid function을 처리하여 구한다.
parameter w,b로 우리가 예측한 ŷ값이 실제 label y 값과 비슷해야 하는 데 이 때 지표를 Loss function으로 정의한다.
sum of squares error는 L(ŷ,y)=(ŷ-y)^2/2로 정의하는데, 이렇게 정의한 L(ŷ,y)는 non-convex 하기 때문에 적절한 loss function은 아니다.
따라서 logistic regression에서는 log 함수를 이용하여 L(ŷ,y)=-[ylogŷ+(1-y)log(1-ŷ)] 이렇게 loss function을 정의한다.
y=1일 때 ŷ=1이면 loss function이 작아야 하고 ŷ=0이면 loss function이 커야 한다.
반대로 y=0일 때 ŷ=0이면 loss function이 작아야 하고 ŷ=1이면 loss function이 커야 한다.
위처럼 log 함수를 정의하여 loss function을 정의하면, y=1이고 ŷ=1이면 L=0, ŷ=0이면 L은 무한대, y=0이고 ŷ=0이면 L=0, ŷ=1이면 L은 무한대가 나온다.
Loss function은 하나의 example에 대한 것이고 m개의 example에 대해 loss function을 평균 낸 것이 cost function이고 이를 J(w,b)로 표기한다. cost function을 결정하는 데는 parameter이 필요하기 때문에 요인으로 w,b가 들어간다.
Gradient Descent

가장 작은 J를 만드는 w,b를 찾아야 한다.

위에서 정의한 cost function은 convex 하기 때문에 미분값이 0이 되는 지점에서 J의 global minimum을 찾을 수 있다. 따라서 주어진 parameter에 대해 J를 결정하는 parameter 값을 조금씩 변화시켜가면서 parameter의 변화가 0이 되는 (미분값이 0이 되는) 지점을 찾아야 한다.
(derivatives 내용은 생략)
Logistic Regression Gradient Descent

(하나의 example에 대해) input인 x1, x2가 있을 때 loss function을 최소화 해주는 parameter w1,w2,b 값을 gradient descent로 찾아주어야 하고 이 때 loss function에 대한 parameter들의 derivatives를 구해줘야 한다.
dz = dL/dz = (dL/da)*(da/dz) = a-y
da = dL/da = -y/a + (1-y)/(1-a)
dw1 = ∂L/∂w1=(dL/dz)*(dz/dw1) = x1 * dz
dw2 = ∂L/∂w2=(dL/dz)*(dz/dw2) = x2 * dz
db = ∂L/∂b = (dL/dz)*1 = dz
이렇게 찾은 parameter w1,w2,b에 대한 derivatives로 w1,w2,b를 갱신해줘야 한다.
w1 := w1 - α * dw1
w2 := w2 - α * dw2
b := b - α * db
Gradient Descent for m examples


이번엔 한 개의 example이 아닌 m개의 example에 대해 gradient descent로 parameter들을 갱신하는 방법을 알아보겠다. x에 대한 feature가 n개(x1, x2, ... ,xn) 있으면 w도 w1, w2, ... ,wn으로 n개가 있다. b는 한 개만 있다. (w1*x1+w2*x2+...+wn*xn+b로 계산하기 때문)
for 문을 example을 하나하나 돌려주겠다. J는 각 example에서 lost function을 평균 내 준 것이니까 각 example마다 loss를 계산하여 더해주고(J+=-[y(i)log a(i)+(1-y(i))log(1-a(i)]) 나중에 for문을 빠져나와서 m으로 나눠주겠다.(J/=m)
dz(i)는 a(i)-y(i)로 계산되고, dw1(i),dw2(i)도 x1(i)*dz(i),x2(i)*dz(i)로 계산되는데 어차피 w1,w2를 update 할 때 각각의 i에 대해서 계속 빼는 형태이므로 for문을 돌면서 계속 더해준 다음에 for문이 끝나고 나서 m으로 나눠주고 한 번에 w1,w2를 update 해준다. db(i)도 마찬가지.
'딥러닝 > DeepLearning.ai' 카테고리의 다른 글
| 3주차. Programming assignment (0) | 2021.02.05 |
|---|---|
| 3주차. Shallow Neural Network (0) | 2021.02.04 |
| 2주차. Programming: Logistic Regression with Neural Network mindset (0) | 2021.02.03 |
| 2주차. Vectorization (0) | 2021.02.03 |
| 1주차. Deep Learning introduction (0) | 2021.02.02 |



