Resampling
데이터의 크기가 작은 경우 데이터셋의 크기를 늘리는 방법
1) CV (Cross Validation)

dataset을 k fold로 쪼개어 하나의 fold를 validation fold로, 나머지를 training fold로 사용한다. training fold로 model을 생성하고 validation fold로 모델을 평가한다. k번의 iteration이 끝난 후 성능을 평균내어 성능을 평가한다.
2) BootStrap

- 앙상블(ensemble): 여러 학습 알고리즘을 사용하여 학습 모델을 생성하는 것으로, 단일 알고리즘을 사용했을 때보다 성능이 높다. bootstrap은 앙상블 기법 중 하나이고 연산량이 많다.
- BootStrap: original sample을 하나의 모집단처럼 생각하여, 여기서 표본 집단을 (중복을 허용하여) 여러 번 복원추출 하고 구해진 통계치를 평균을 내서 사용한다. -> random sampling으로 train set이 적다는 문제점을 극복함.
- 한 번 뽑힌 샘플이 또 뽑힐 수 있다.
- 한 번도 뽑히지 않은 샘플이 존재할 수 있다.
Bagging
| categorical data | continuous data |
 |
 |
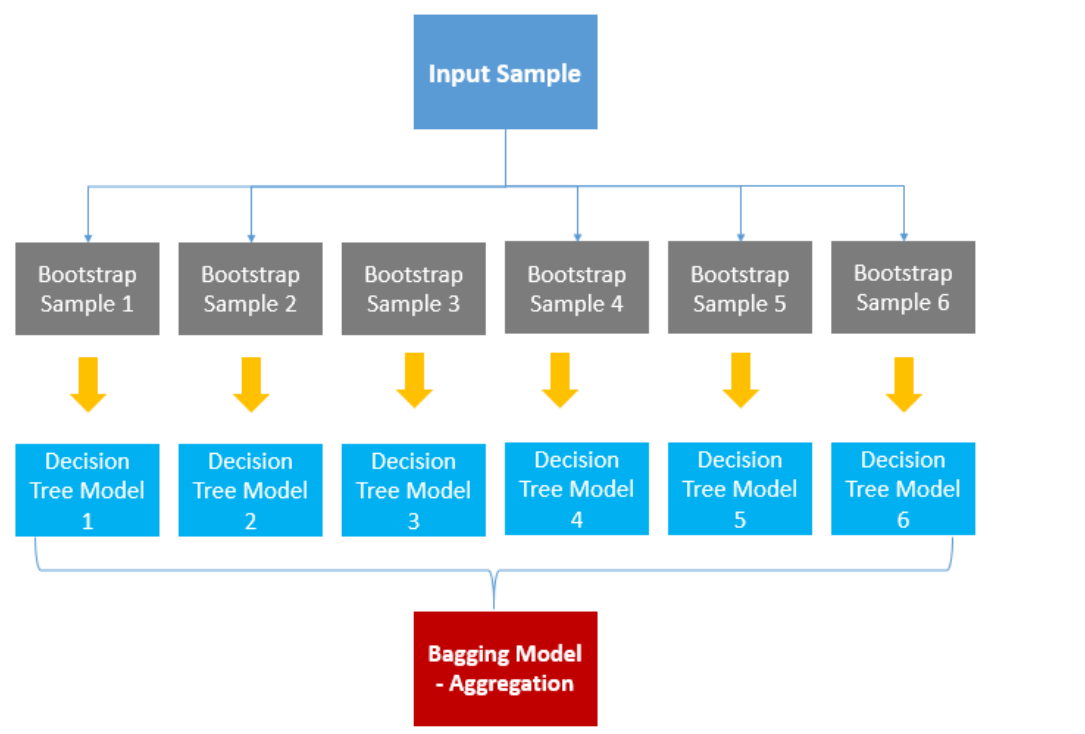
- 동일한 model을 학습시킨 bootstrap을 모아서(aggregate) 학습된 모델의 예측변수들을 집계한 모델
=> 단일 model을 사용했을 때보다 variance를 줄일 수 있다.
- bootstrap을 통해 B개의 training set을 만들고 B개의 tree를 만들어 평균내면 variance가 줄어들 것이다.

단일 model을 쓸 경우 variance
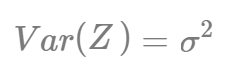
B개의 model을 bagging으로 사용할 경우 variance

model들끼리 독립이라고 가정한다면 cov가 0이 되어 확실히 모델의 분산이 줄어들테지만, 같은 original sample에서 추출한 표본들로 만든 model들이기 때문에 model들끼리 독립이라고 할 수 없다.
=> Decorrelated Tree로 model끼리 covariance를 줄이자! 이 방법을 Random Forest에서 수행하고 있다.
Random Forest
|
Decision Tree |
Random Forest |
|
- "Greedy Algorithm Search" - 가지를 나눌 때 모든 p개의 feature에 대해 모두 분리해보고 mse를 계산하여 mse가 가장 낮아지는 쪽으로 가지를 나눈다. |
- model을 생성할 때 p개의 feature 중 M개를 무작위로 선택하여 트리를 분할함 ex) model 1은 x1, x3, x7로, model 2는 x1, x8, x9로 생성 |
Decorrelated Tree
- 각 tree에서 model 생성시 p개의 feature 중 M개만을 고려하여 트리를 분할함
- 만약 한 가지 예측변수가 매우 강력한 예측 변수라면 greedy하게 만들어진 tree는 가장 강력한 하나의 변수를 top split으로 삼고 있을 것이고 이로 인해 tree들이 매우 비슷하게 만들어지고, 전체 variance를 줄이지 못한다.
- decorrelated 하게 tree를 분할하면, 어떤 tree는 강력한 변수를 포함하고 있지만, 어떤 tree는 그 변수보다 덜 중요하지만 어느정도 모델에 기여하는 변수가 모델을 예측하는데 기여하게 된다. 곧 전체 variance가 줄어들 것이다.
OOB sample
bagging을 통해 표본을 추출하면 한 번도 뽑히지 못한 sample이 존재한다. 이러한 sample을 OOB(Out-of-Bag) sample 이라고 한다. 이 sample들을 validation set으로 사용하여 test error를 측정하거나 feature importance를 계산할 수 있다.
Feature Importance 계산
- variable이 random하게 선택되었을 때 MSE가 얼마나 오르는 지로 평가할 수 있다.

- Xi변수의 feature importance를 알고자 할 때, original OOB sample - ①에서 Xi의 값들의 순서를 뒤바꿔서 새롭게 OOB sample을 만든다. - ② 즉, ②에서는 Xi와 Y 사이의 관계가 무너졌다.
- ①의 MSE와 ②의 MSE를 비교한다.
- ①<<<② : Xi와 Y의 관계가 유의하다. (Xi와 Y의 관계를 무너뜨렸을 때 성능이 나빠졌으므로)
- ① ≒ ② : Xi와 Y의 관계가 유의하지 않다. Y를 예측하는 데 Xi가 중요한 변수가 아니다.

단, feature importance가 높다는 말이 Xi가 Y와 함수적 관계가 있다는 말이 아니다.
Xi가 random forest에서 Y를 예측하는 데에 중요한 변수라는 뜻이지, 다른 알고리즘에 적용했을 때에도 그럴 것이라는 게 아님.
Voting
| Bagging | Voting |
하나의 알고리즘 내에서 서로 다른 sample을 조합하여 투표 - classification: voting - regresson: average로 집계
|
여러 알고리즘 모델에서 도출한 결과물을 투표 |
 |
 |
| voting | |
| hard vote | soft vote |
| 결과물에 대한 최종 값을 투표로 결정 | 최종 결과물이 나올 확률값을 다 더하여 최종 결과물에 대한 각각의 확률로 생각하여 결정 |
 |
 |
| classifier 1,3,4에서 y=1로 예측, classifer 2에서 y=0으로 예측 => 다수결에 따라 y=1로 예측 |
- classifer 1~4에서 y=1일 확률에 대한 평균: (0.7+0.2+0.8+0.9)/4=0.65 - y=0일 확률에 대한 평균: (0.3+0.8+0.2+0.1)/4=0.35 =>y=1로 예측 |
'머신러닝 > 분석 base' 카테고리의 다른 글
| Resnet (0) | 2021.02.23 |
|---|---|
| Boosting & Adaboost (0) | 2021.02.09 |
| Bagging & Random Forest : Programming (0) | 2021.02.09 |
| SVM: programming (0) | 2021.02.08 |
| SVM (Support Vector Machine) (0) | 2021.02.08 |


