https://www.youtube.com/watch?v=kr-7PXLefyc&list=PLKKkeayRo4PWyV8Gr-RcbWcis26ltIyMN&index=5
본 게시물은 '인과추론을 위한 데이터과학' Session 2를 참고하여 작성했습니다.
[2-1] 인과추론을 위한 연구 디자인

- Meta-Analysis: 여러 인과추론의 결과를 종합적으로 분석하는 방법론. 여러 데이터셋 → 반복적인 인과관계 → 여러 인과적 근거를 종합
- Randomized Experiment (Randomized Controlled Trial, RCT): 단일 방법론
- Quasi-Experiment: RCT를 실제로 수행할 수 없는 환경에서 준실험 방법
- Instrumental Variable: 인위적인 도구변수(인과추론을 방해하는 내생성 Endogenous을 제거하기 위한 도구)를 사용
- “Designed” Regression (w/ Casual Diagram): 적절한 통제변수의 디자인으로 회귀분석
- Regression: 통제변수에 대한 적절한 디자인이 없을 땐, 통제변수를 많이 포함한다고 해도 선택편향 제거하기 힘듦
[Session 2-2] 인과추론의 정석: 무작위 통제실험 (Randomized Controlled Trial)
Gold Standard of Casual Inference: Random Assignment
law of large numbers → random assignment: treatment group과 control group이 유사한 특성을 가진다.(검정 필요) → 비교 가능해짐
ex. 교실에 태블릿, 노트북 허용시 성적에 차이가 나는가?
treatment(교실 내에서 랩탑 or 타블렛 사용 여부) 제외하고 나머지 모든 요인에 대해 비교 가능해야 함
Baseline Characteristic은 그룹별로 동질해야하고 Observed computer use는 실험 설계에 따라 차이가 나야 함 (합당함) → 그룹별 차이는 treatment의 인과 효과라고 볼 수 있음.
- 장점: 복잡한 통계 모형이 필요하지 않음
- 단점: 실험 설계가 까다로울 수 있음
안좋은 실험 연구 예시
- Baseline (아무 처리도 하지 않은 경우)이 Control 그룹의 염증 지수 <Treatment 그룹의 염증 지수
- 건강한 사람이 Control 그룹에, 건강하지 않은 사람이 Treatment 그룹에 많음
- Randomized Assignment가 제대로 이루어지지 않았음
- 건강한 사람이 Control 그룹에: 약을 안먹어도 염증지수 크게 변하지 않을 것
- 건강하지 않은 사람이 Treatment 그룹에: 4주 후, 8주 후에 나은 이유가 약때문이 아니라 자연치유 일 수도 있음
주의사항
Randomized Assignment 이후에 두 그룹이 균질적인지 & 다른 요인에 의해 영향을 받을 수 있는 지 확인해야 함
[2-3] Quasi-Experiment: 실험아닌, 실험같은 준실험

- 인과추론이 목적이고, ramdom assignment가 가능하다
- RCT
- random assignment가 불가능한 상황.
- treatment가 확실하게 정의되고 control group과 treatment를 분명히 구분할 수 있는 경우
- treatment의 전후를 관찰할 수 있는 경우
- 실험 대상이 treatment 여부를 선택할 수 있는 경우: Self-Selection
- treatment가 임의적인 threshold / cutoff에 의해 결정되는 경우:Discontinuity
- treatment의 전후를 관찰할 수 있는 경우
- treatment가 확실하게 정의되고 control group과 treatment를 분명히 구분할 수 있는 경우
Quasi-Experiment
- Quasi-Experiment는 random assignment를 수행할 수 없는 경우에 exogenous shok, self-selection, arbitrary cutoff 등의 방법을 이용해서 randomized-experiment를 따라하는 방법이다.
- Quasi-Experiment의 목표는 CETERIS PARIBUS를 만족하는 비교 가능한 control group을 만들어서 control group에서 counterfactual을 추론하는 것이다.
ex) Exogenous Shock

- 연구 주제: 지역의 금융에 대한 접근성(access to local finance)이 창업(firm formation)에 미치는 인과적인 효과가 있는가?
- 한계점: 변수를 통제하기 어려움
- 창업 정도를 판단하기 위해 지역별로 local finance를 직접 통제할 수 없음.
- ⇒ shale boom을 natural shock으로 설정하여 Exogeneous shock 실험 설계
- Exogeneous shock
- treatment group: shale boom O -> local finance O -> firm formation 측정
- control group: shale boom X -> local finance X -> firm formation 측정
- Exogeneous shock 실험의 장점: control group과 treatment group에서 random한 효과가 어느 정도 보장된다.
- exogenous shock은 어디서 어떻게 발생할지 알수없음(어느 지역에 shale boom이 나타날 지 여부는 random하게 발생) → 어느정도 randomized assignment를 가정할 수 있음 → treatment group과 control group에 통제변수가 비슷할 것 ⇒ natural experiment
ex) Self-Selection
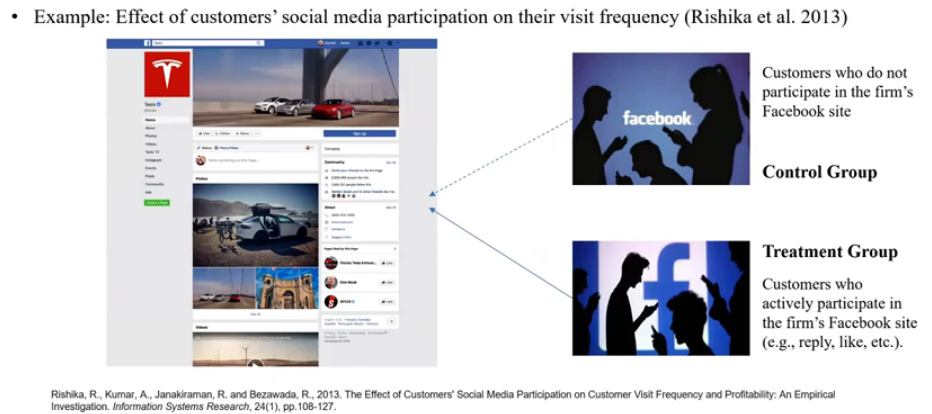
- 연구 주제: 소비자가 기업 페이스북에 참여(like, reply, ...)하는 것이 그 소비자가 기업의 웹사이트 방문 빈도에 인과적인 영향을 미치는가?
- Treatment: 기업의 페이스북에 참여
- Control group: 기업의 페이스북에 참여하지 않는 소비자들
- Treatment group: 기업의 페이스북에 참여하는 소비자들
- 연구자의 의도나 외부 요인에 의해 Control/Treatment가 배정되는 것이 아니라, 소비자가 직접 선택
- Self-Selection: 소비자의 자발적인 선택(페이스북에 참여하는지 여부)에 따라 treatment group과 control group을 쉽게 나눌 수 있음. [Control/Treatment 그룹에 페이스북에서 참여할 지(treatment) 여부를 선택함]
- 단점: Control/Treatment에 속하는 소비자의 의도를 알 수 없음 → 두 집단이 정말로 비교 가능한지 알 수 없음 → 엄밀하게 ceteris paribus 점검해야 함

- 연구 주제: SNS(트위터)에서 친구의 입소문이 어떤 영향을 미치는가?
- 내가 기업의 홍보성 트윗을 리트윗하면, 나와 기업을 모두 팔로잉 한 사람들에게만 트윗이 보임
- treatment: 내 SNS 친구가 리트윗하는 행위 (입소문)
- treatment group: 내 팔로워이면서 기업을 팔로잉한 사람 (메시지가 보임)
- control group: 내 팔로워이지만 기업을 팔로잉하지 않은 사람 (메시지가 보이지 않음)
- 비교적 안전한 Self-Selection
- treat,control group이 모두 나의 팔로워라서 두 집단의 특성이 유사할 것
- [Control/Treatment 그룹이 리트윗 여부(Treatment)를 선택하는 것이 아님]
- 팔로워들이 리트윗하는 treatment 자체를 선택하는 것이 아님, 간접적으로 연구 대상의 선택에 의해 tr이 결정됨
Exogenous Shok과 Self-Selection의 차이점

- Exogenous Shock: Ceteris Paribus 만족이 쉬움
- self-selection: 엄밀한 Ceteris Paribus 증명이 필요함
ex) Discontinuity
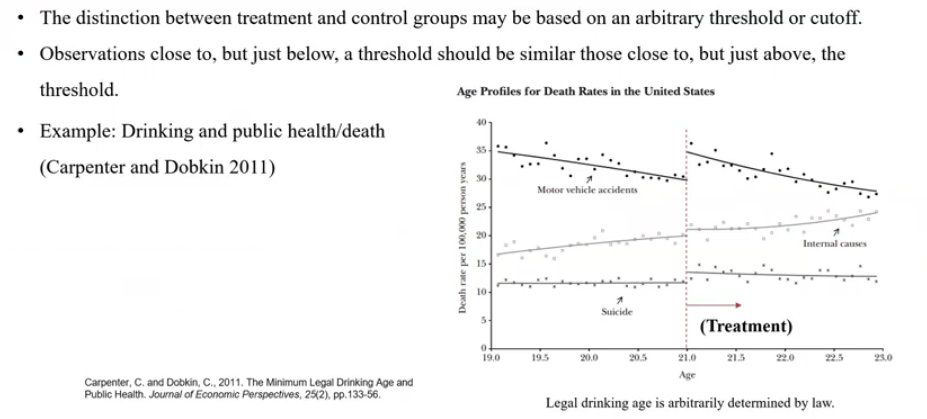
- 연구 주제: 음주와 건강 사이의 인과관계
- 21세(미국의 음주 가능 나이, arbitrary threshold or cutoff) 전후에 사망률에 차이가 생긴다면, 음주가 미치는 인과적인 효과라고 볼 수 있음.
- control group: 21세 이전, 음주 불가
- treatment group: 21세 이후, 음주 가능
[2-4] 준실험 분석도구: Difference-in-Difference & Regression Discontinuity
Difference-in-Difference(DID) - 이중차분법

- TA: treatment 그룹, t2 시점에서, treatment 효과
- TB: treatment 그룹, t1 시점에서, treatment X 효과
- TA’( = Counterfactual): treatment 그룹, t2시점에서, treatment X 효과 (관찰 불가능)
- CA: control 그룹, t1 시점, treatment X 효과
- CB: control 그룹, t2 시점, treatment O 효과
- CA-CB: control 그룹에서 시점의 차이
- TA-TB: (treatment 그룹에서 시점의 차이) + (treatment 여부의 차이)
- TA-TA’: treatment 그룹에서 treatment 여부의 차이
- TB + (TA’-TB): (treatment 그룹, t1 시점, treatment X 효과) + (treatment 그룹, t1시점~t2시점의 treatment X 효과의 변화량)
- TB + (CA-CB): (treatment 그룹, t1 시점, treatment X 효과) + (control 그룹, t1시점~t2시점의 treatment X 효과의 변화량)
- (TA-TB) - (CA-CB): (treatment 그룹에서 시점의 차이) - (control 그룹에서 시점의 차이) + (treatment 그룹에서 treatment 여부의 차이)
- if (treatment 그룹에서 시점의 차이) - (control 그룹에서 시점의 차이) = 0이라고 한다면 (treatment 그룹에서 시간에 따른 변화량 = control 그룹에서 시간에 따른 변화량), DID estimator를 관찰 불가능한 TA-TA’ 대신 (TA-TB) - (CA-CB)으로 추정 가능
- DID estimator = TA - TA’ ← TA-[TB+(CA-CB)]
Identification Assumption: Research Design에서 selection bias 없앨 수 있는 가정
Parallel Trends Assumption: DID analysis에서의 Identification Assumption
- treatment가 없을 때 treatment 그룹과 control 그룹이 동일해야 한다 (X)
- treatment가 없을 때 treatment 그룹과 control 그룹에서 시간에 따른 변화량과 변화 패턴만 유사하면 된다 (O)
- treatment가 없을 때 treatment 그룹과 control 그룹이 시간에 따라 평행하게 변화해야 한다. (O) ⇒ “Parallel Trends assumption” → why?
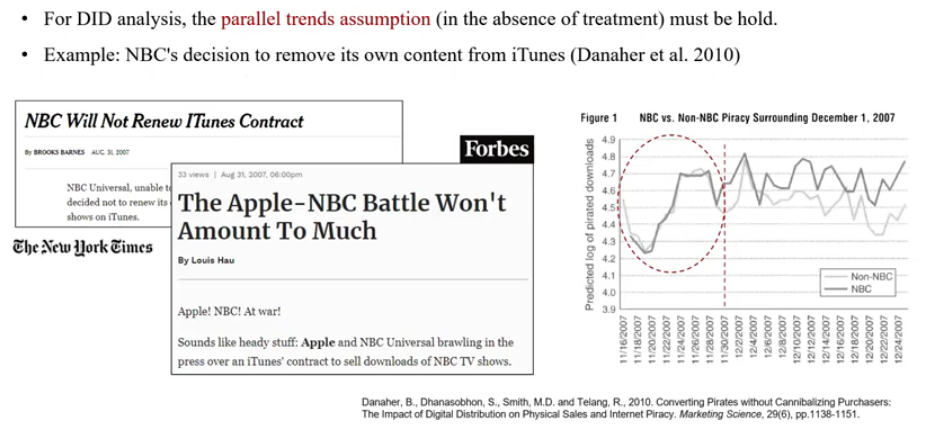
- 연구 주제: 합법적인 디지털 유통 채널이 있으면 불법다운로드가 줄어드는 인과적 효과가 있는가?
- Exogenous Shock: ITunes에서 t시점에 NBC 컨텐츠를 내림
- Treatment group과 action: NBC 채널의 t시점 이후의 불법다운로드 수
- Control group과 action: ABC, CBS 및 Fox 채널의 t시점 이후의 불법다운로드 수
- DID analysis: Treatment group과 Control group의 시점에 따른 불법복제의 수치 비교
- Parallel Trends assumption: 사건 이전에 (t시점 이전) NBC와 non-NBC의 불법다운로드의 예측 로그가 “평행” (시간에 따른 변화량 비슷)
- 13:12 Parallel Trends assumption을 만족한다면 treatment 이전의 control 그룹과 treatment 그룹 간 시간에 따른 변화량이 비슷하기때문에 randomized assumption을 만족하는듯한 효과가 나타나기 때문에 인과추론에서 유리한 도구가 된다 → why?
Matching Techniques
- Quasi에서 연구자가 직접 treatment를 결정할 수 있다면, ceteris paribus를 쉽게 만족할 것이다.
- 하지만 연구자가 직접 treatment를 결정할 수 없고, 외부적으로 control과 treatment group이 결정된다면 → ceteris paribus을 만족하지 않는 경우가 있을 수도 있고 → comparable control group이 없어서 counterfactual을 추론하기 어려울 수 있다. → MATCHING 기법 사용하자!
- 변수들의 값이 평균적으로 유사한 샘플들만 매칭해주는 기법 (남자~남자, 고소득~고소득, ...)
- 목표: treatment 그룹에서 treatment X (counterfactual)과 control 그룹을 유사하게 만들어주고자
- Propensity Score Matching (PSM)
- Coarsened Exact Matching (CEM)
PSM
propensity 계산 → propensity가 유사한 그룹끼리 계산
propensity score: treatment 그룹에 속할 확률, logit/probit model로 예측

'계량경제학 > 인과추론의 데이터과학' 카테고리의 다른 글
| 인과추론을 위한 회귀분석 - Polynomials (1) | 2022.09.21 |
|---|---|
| 인과추론을 위한 회귀분석 - Discrete Variable (2) | 2022.09.21 |
| 인과추론을 위한 회귀분석 - 회귀분석의 개요 (0) | 2022.09.21 |
| Causal Diagram (1) | 2022.07.30 |
| Instrumental Variable, Control Variable, Selection Model (0) | 2022.07.30 |


